Из системы (2.28) нетрудно получить дифференциальное уравнение для фазовых траекторий в виде

+

(4.30)

Уравнение (4.30) можно решить графически (см. § 4.5) и получить траектории, показанные на рис. 4.15, а и 4.15, б и зависящие от знака корня. Как и в первом случае, положение равновесия для этой системы есть узел.

Случай 5. Будем считать, что один или оба собственных значения нулевые. В этом случае фазовые портреты, в некотором смысле вырожденные, и положения равновесия располагаются не только в начале координат. Можно выделить два случая:

1. Один из корней нулевой, тогда уравнения (4.21) принимают вид

0 7\jX2-

В этом случае каждая точка (Xi, Xg) = (с, 0) является положением равновесия, где с - произвольная постоянная.

2. Оба собственных значения нулевые. Тогда для канонической формы {4.28) при Я, = О получим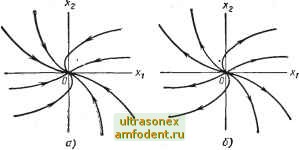

Рис. 4.15. Вид фазовых траекторий для системы второго порядка, представленной в виде уравнения (4.28):

а :- при Я < 0: б -- при Я > О Xl - kx; 2 = О,

откуда имеем

Xl (О = 10 + kxt; xzit) = X

Каждая точка (xi, л:2) = (с, 0) является положением равновесия, где с - произвольная постоянная. Если к тому же й = О, то х = 0; Х2 = О и любая точка фазовой плоскости является точкой равновесия. Фазовые траектории для перечисленных случаев показаны на рис. 4.16. Отметим, что для любого графика каждая точка оси х является положением равновесия.

Построив траектории для канонической системы координат, преобразуем их к нормальной системе координат. Как уже было отмечено, матрица преобразования в этом случае не является ортогональной.

В качестве примера рассмотрим случай различных действительных по-

люсОв. Тогда нормальные координаты преобразованием

f/i 1 Г 1 1 Xl

. f/2 J L 1 2 J 1:2

Из уравнения (4.31) следуег, что линия х = О преобразуется в прямую У2 = iUi, в то время как прямая Х2 = О переходит в прямую г/2 = li/i-В общем случае эти прямые не ортогональны. Тем не менее общий характер фазовых траекторий вдоль этих линий сохраняется. Эта зависимость позволяет построить узлы и седловые точки на фазовой плоскости в нормальных

связаны с каноническими

(4.31)

координатах. Допустим, что начало координат - устойчивый узел. Это означает, что Xi <0 (t = 1, 2). Пусть <Я,2 <0. В канонических координатах все траектории в конце концов касаются оси (см. рис. 4.12, а), и, следовательно, при переходе к нормальным координатам они будут

X у X 5 Хч

Л;

а) S) В)

Рис. 4.16. -Вид фазовых траекторий в канонических координатах для систем второго порядка: а - при Я, = 0; Я, < 0; б - при Я, = 0: Яв > 0; в - при Я1 = Я = О

касательны к линии, соответствующей оси Х2 (или к линии х = 0), т. е. к прямой у2 = кУг- Кроме того, ни одна траектория не пересекает ни прямой Хх - О, ни прямой Х2 = 0. С учетом сказанного нетрудно убедиться, что фазовый портрет на рис. 4.17, а есть образ фазового портрета рис. 4.12, а, но в нормальныхчкоординатах.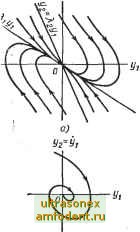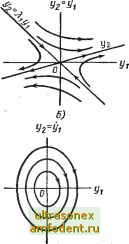

В) г)

Рис. 4.17. Виды фазовых траекторий в нормальных координатах для систем второго порядка:

о-при я, < о, /,2 < 0; б-при я, < 0; Я > 0; в-при Xt= Re Я -)-+ jlm Я; Ъ.2 - Re Я-jlm Я, где Re Я < 0; г-тот же случай, что и в, но при Re Я = О

В случае седловой точки (см. рис. 4.13), когда <; О и Я,2 [> О, видно, что оси Xi и Х2 являются асимптотами гиперболических траекторий. Это свойство сохраняется и после выполнения преобразования (4.31). Фазовый портрет такой системы в нормальных координатах показан на рис. 4.17, б.

Если %i (i = 1,2) - комплексно-сопряженные корни, то нетрудно видеть, что фазовый портрет системы в нормальных координатах будет таким, как на рис. 4.17, в (при Re \ < 0). Если все корни чисто мнимые, то фазовый портрет изображен на рис. 4.17, г.

Знание поведения траекторий линейных систем вблизи начала координат важно по многим причинам и в первую очередь потому, что это позволяет судить и о траекториях нелинейных систем вблизи их положений равновесия. Для того чтобы воспользоваться полученными результатами, достаточно лишь линеаризовать нелинейную систему. Методы линеаризации более подробно будут изложены в гл. 5.

4.4. ПРЕДЕЛЬНЫЕ ЦИКЛЫ И ДРУГИЕ ВИДЫ ТРАЕКТОРИЙ ДВИЖЕНИЯ АВТОНОМНЫХ НЕЛИНЕЙНЫХ СИСТЕМ

Невырожденные линейные автономные системы обладают рядом весьма привлекательных свойств. Во-первых, в таких системах есть лишь одно положение равновесия, во-вторых, их поведение вблизи положения равновесия определяет качественную картину траекторий во всем фазовом пространстве. Аналогичные свойства, к сожалению, не присущи нелинейным автономным системам. Мы отметим лишь два явления, которые отличают нелинейные автономные явления от линейных, а именно: существование предельных циклов и различный характер движения в разных областях фазового пространства для одной и той же системы.

В линейных автономных системах второго порядка колебания могут существовать лишь при единственном сочетании параметров. Малое отклонение в значениях параметров приводит к затуханию автоколебаний. Если в системе существуют колебания, то фазовыми траекториями такой системы являются замкнутые кривые с центром в начале координат, как это показано на рис. 4.17, г. Расстояние замкнутой траектории и, следовательно, амплитуда автоколебаний не остаются постоянными при изменении начальных условий.

В нелинейных автономных системах колебания также могут иметь место. Более интересно то, что в этом случае параметры колебаний могут не зависеть от начальных условий. Такие колебания определяют в системе предельный цикл, который и используется для реализации на практике таких устройств, как генераторы. Колебания в предельном цикле, как правило, мало чувствительны к изменению параметров, а иногда существует целая область изменения параметров, внутри которой колебания не срываются.

Если не быть слишком строгим, то предельный цикл в системе можно отождествить с замкнутой кривой G в фазовом пространстве, обладающей одним из следующих свойств:

1. Все траектории системы в окрестности G постепенно приближаются к этой замкнутой кривой при - оо (рис. 4.18, а).

2. Любая траектория, начинаясь произвольно близко к G, удаляется от G при t-*oo (рис. 4.18, б).

3. Все траектории в окрестности G разделяются на два взаимно исключающих семейства. Траектории одного семейства направлены к G при t -у оо; остальные траектории удаляются от G при - оо (рис. 4.18, б).

Как правило, предельный цикл первого типа называется устойчивым предельным циклом; второго типа - неустойчивым пр,едельным циклом и, наконец, третьего типа - полуустойчивым предельным циклом. Как мы покажем в следующей главе, одно слово устойчивый еще не определяет в полной мере характера устойчивости. Для характеристики предельных