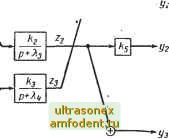
тот же порядок, что и знаменатель, то можно воспользоваться методом, изложенным в п. 4 § 2.5. При этом параметры kg, k, . . ., k рассматриваются как функции времени.

Можно показать *, что при

где G = 1, и

М (р, О = S (t) pi,

имеем

i-l i-m

ko{i) = bo{ty, ki(t) = bi{t)- j: S C+bG, ft(Opm(0- (2.44) Здесь символ Cn обозначает число сочетаний из п элементов по г, т. ё.

с;; =

r\(n-r)l

(2.45)

2.8. УРАВНЕНИЯ СОСТОЯНИЯ СИСТЕМЫ ДЛЯ СЛУЧАЯ

НЕСКОЛЬКИХ ВХОДОВ и выходов

Принимая во внимание все изложенное выше, нетрудно получить уравнения состояния для системы с несколькими входами и выходами. В данном случае для характеристики системы вместо векторов b я с должны использоваться матрицы В п Сщ

Пример 2.7. Рассмотрим систему с двумя входами и тремя выходами (рис. 2.14). Заметим, что система имеет шестой порядок. Следуя методу нормальных координат, принимаем в качестве переменных состояния

* .

Xi = Zi, Х2= Xi = Zii Хз = Za; Хд = z; х г; Хд = х- z.

Основываясь на приведенной схеме, получим

х = Ах-\-Ви; у = Сх. где

О 10

о о о о

Рис. 2.14. Структурная схема, рассматриваемая в примере 2.7

- О О

О -\ о о о о

о о о 1

о -К

1 0 0 1 0 0

о о о о о

0 0 1 0 10

* См. 1206] стр. 357 и [ИЗ] стр. 190.

2.9. ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЬНИЕ ДЛЯ СТАЦИОНАРНЫХ СИСТЕМ

Хорошо известно, что для стационарных систем вида (2.14) уравнение

L (К) = О, (2.46)

где К - комплексная переменная - является характеристическим уравнением системы, а корни уравнения (2.46) - полюсы системы. Если система (2.14) описывается уравнением состояния

х==Ах + Ви, (2.47)

то можно показать (упражнение для самостоятельного выполнения), что характеристическое уравнение можно записать в следующей детерминантной форме *: .

Л-Х/ = 0. (2.48)

Следовательно,

Ь{К)\А - и\.

Корни уравнения (2.48) [и, следовательно, полюсы системы (2.34)] известны в матричном исчислении как собственные значения или как характеристические числа матрицы А. Уравнение (2.48) получается при нахождении такого вектора V ц пространстве состояний, который преобразуется матрицей А с точностью до постоянного множителя сам в себя. Другими словами,

Av = Kv, (2.49)

где X, как и в случае уравнения (2.48),- скалярная комплексная величина. Векторы, удовлетворяющие уравнению (2.49), называются собственными векторами матрицы А. Более полное рассмотрение основ матричного исчисления приводится в приложении I.

2.10. КРАТКОЕ СОДЕРЖАНИЕ

Почти все системы, описываемые дифференциальными уравнениями, можно характеризовать векторными уравнениями (2.5):

x=f{x,u,ty, y = g(x,u,t).

В частности, линейные системы описываются следующими матричными уравнениями (2.8):

x = A(t)x + B{t)u; y = C{t)x + D{f)u.

Уравнения (2.5) и (2.8) известны как уравнения состояния системы. Вид этих уравнений, вообще говоря, не однозначен. Выбор той или иной формы их записи зависит от исследуемой задачи.

Различные способы, выбора переменных состояния рассмотрены в §§-2.5 и 2.6.

* Это справедливо лишь, когда в функции G (р) не происходит сокращения нуля с полюсом. Сокращение нуля и полюса можно рассматривать как случайное обстоятельство, когда система п-го порядка ведет себя для стороннего наблюдателя при нулевых начальных условиях, как система (и - 1)-го порядка. Когда это имеет место, вычет сократившегося полюса равен нулю, так что каноническая схема передачи сигналов должна иметь одну прямую цепь разомкнутой. Если данную ветвь не учитывать, то получим матрицу А порядка (и - 1) X (и - 1). Случай сокращения полюса и нуля рассмотрим в следующей главе при введении понятия управляемости системы.

в случае линейных систем с постоянными параметрами особое значение имеют следующие два способа:

1) нормальная форма, когда элементами вектора состояния являются выходной сигнал и его первые п - 1 производные;

2) каноническая форма, когда координаты х представляют составляющие собственных колебаний.

В случае линейных систем с переменными параметрами нормальная форма представления возможна, а каноническая невозможна.

Если имеется динамика, соответствующая числителю [т. е. полином М (р, t) в выражении (2.12) или полином М (р) в выражении (.2.14) не сводятся к постоянным величинам], получение нормальной формы представления усложняется. В этом случае необходимо вводить переменную х i, являющуюся некоторой линейной комбинацией выходного и входного сигналов. В качестве переменных состояния используют величину Xi и ее ft - 1 производные (см. пример 2.6 в § 2.7). При анализе систем с несколькими входами и выходами их также целесообразно описать через переменные состояния.

2.11. ЗАДАЧИ ДЛЯ УПРАЖНЕНИЙ

2.1. Получите уравнение состояния для цепи с бесконечной полосой пропускания, описываемой передаточной функцией

F(p)

U(p) 1+Tip

в которое не входили бы производные от и. Представьте результаты в виде схемы передачи сигналов от и к у.

2.2. Для системы, рассмотренной в примере 2.3, получите уравнения состояния в нормальной форме и найдите матрицу, преобразующую канонический вектор состояния лга) в нормальный вектор состояния {ух> Уй-

2.3. Покажите, что для линейной системы с передаточной функцией

oip)--.-

уравнения состояния в нормальной форме имеют вид

Xn-l

х

-G -а 1 -йп-г - 2 - fli - К -

где выходной сигнал определяется выражением у = х-- kgU, а постоянные ki - выражениями k = b ;

i-l

ki = 6,- - £ ( = 1..... )

2.4. Рассмсугрите линейную стационарную систему с одним входом и {t) и одним выходом у (t), связь между входом и выходом которой определяется соотношениями

(р+1)(р + 4)

.y{t)=G(p)u{t); G{p) = -

(р-Ь)Чр + 2Г