Если = а sin (со/ + Ф), а Xia = Р sin (со/ -j- Фа), то

-2 а -2 р

11 = ; 12 = -; 1112=cos (Ф1-Ф2);

(6.47)

к тому же

Xiif= J I/ (а sin (со/ + Ф), р sin (со/ + Ф) ] sin (со/ + Ф) d (со/); (6.48а) о

W=2 f [Ис51п(сй/ + Ф1), Р51п(сй/+Фа)]81п(сй/+Ф2)а(сйО.. (6.4 о

Подставляя выражения (6.47) и (6.48) в соотношения (6.46а, б), можно определить эквивалентные передаточные функции Л/ц и Л/, а-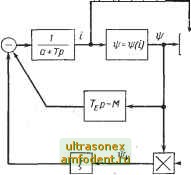

b*TjP

Рис. 6.13. Структурная схема системы: сериесный электродвигатель с генератором (для примера 6.8)

Мы уже рассмотрели пример нелинейности с двумя входными сигналами, входящей в уравнение Ван-дер-Поля (см. § 6.1), которое описывает систему с обратной связью с нелинейным членом, задаваемым соотношением

/ (Xj, Х2) = [1X2X2; Xj = Х2.

Таким образом, справедливо соотношение

(laap

f (%i> Ч2) = -

sin (со/ + Фа) -Ь

-j- sin (со/ + 2Ф1 - Фа) - -i- sin (Зсо/ + + Ф) где без ограничения общности можно положить Ф = 0; тогда получим

Xiif =--g- (хаР cos Фа;

Х=-(1+1созФа).

(6.49)

Поскольку Ха = х, то Фа = -g-. Учитывая это и подставляя соотношения (6.47) и (6.49)

в выражение (6.46), получим = О иЛ/г = - что согласуется с результатами § 6.1 при а = Xj.

Пример 6. 8. Рассмотрим периодические движения в системе с последовательным соединением электродвигателями генератора, которая использовалась как в примере 4.5, так и в примере 5.8.

Уравнениям системы в нормальной форме (5.32) соответствует структурная схема, приведенная на рис. 6.13, откуда видно, что в системе есть три нелинейности.

предположим что высшие гармоники, генерируемые нелинейностями, будут в значительной степени ослабляться линейными элементами системы; так что можно считать сигналы t и V равными

i= to -Ь t sin at; о = vo+ V sin (cot + Ф).

(6.50)

Для получения соотношения между входом и выходом нелинейностей (() и ill) (i) определим коэффициенты передачи Л/ц (io, i); N21 (io, i); Лао (о, i) и N20 {h, i) такие, что

ф (t) = ijjo -Ь ij sin mi +.. -= Лю (io, t) io + Nl (to, i) i sin>/ + Hp (i) i = N20 (io, i) io + N21 (io, 7) t sin tt><-J----.

(6.51) (6.52)

10 0,5

10 i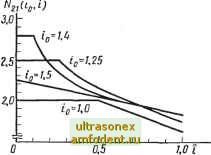

Рис. 6.14. Зависимости Af (io, i) и N2X (to, 0 от i (для примера 6.8)

Третья нелинейность это произведение г]) . На основании выражений (6.50) и (6.51) получим

я]) (i) 0 = (яро + sincoO ( о + V sin (со + Ф) -f - = = ipofo + cos Ф -f fояр sin at + i])oo sin (co -j- Ф) +

+ = Nioiovo + -g- Nxxiv cos Ф + voNxii sin co< + iVioiof sin (m -b Ф) -b ... (6.53)

Эквивалентные передаточные функции для переменной составляющей Ni (io. t) и

Л21 (to, i) можно найти из идеализированной кривой намагничивания (см. рис. 4.20). Это даст нам следующие зависимости:

sin 2а а

Л/ц (to, i) = l+-

l(fo. О = io (I +Л/11) +-acosa --- sin а + sin За , nax - ltol

arccos

, фтах - i io i t ;

(6.54a) (6.546)

(6.55)

фгаах - i io i > i

Кривые Nix иЛ/ai в функции i для различных io показаны на рис. 6.14, а, б:

Удобно изучать постоянную и переменную составляющие раздельно *, чтобы выяснить их влияние на установившееся движение в системе. С этой целью структурную схему рис. 6.13 нужно преобразовать в соответствии с выражениями (6.51) и (6.53) к виду, показанному на рис. 6.15, а и 6.15, б.

Для ( = О постоянная составляющая определяется из соотношения (5.35). Рассмотрим лишь случай \idc\= Mo Кimax, тогда получим

jN (ijHvcos0

idc = dc = io =-±Уу; (го, 0) = 1; 20 (io, 0) = io; Vdc = oo = -- (M - a).

-Л IV

л7 - %

(6.56)

vsin(a}t+0)

M-io-TcPJ

a) 6)

Рис. 6.15, Структурные схемы систем управления примера 6.8:

с - по постоянной составляющей; б - по переменной составляющей

В присутствии автоколебаний значение постоянной составляющей будет медленно изменяться (рис. 6.15, а), чтобы вновь обеспечить равновесие в системе. Такое смещение постоянной составляющей вызовет изменение эквивалентной передаточной функции по переменной составляющей. В рассматриваемом случае для обычно встречающихся численных значений влияние постоянного смещения на амплитуду и частоту автоколебаний несущественно, и им можно пренебречь. В следующем разделе мы рассмотрим случаи, когда необходимо учитывать одновременно переменную и постоянную составляющие.

Исходя из сказанного, можно предположить, что соотношение (6.56) будет справедливо

и при i ф 0. При этом, учитывая лишь первые гармоники в уравнениях (6.51)-(6.53) и используя соотношения (6.56), получим

a(l-Nii)+ {т+ NiiTe)p Но

i sin а)/ f sin (сог-ЬФ)

. .(6.57)

Уравнение (6.57) получено в предположении о существовании гармонических колебаний. Для того чтобы убедиться в справедливости этого предположения, необходимо показать, что характеристическое уравнение для (6.57) имеет чисто мнимые корни. Запишем характеристическое уравнение в следующем виде:

Tj {Т + NiiTe) +[Ь(Т+ Ni-J-e) + а (1 - Я ) Гу] Я + -Ь afc (1 - iVn) + & оЛа1 = 0.

(6.58)

* Здесь г1ринято обозначать idc - постоянная составляющая тока {Прим. ред.).

** Заметим, что при i О и р -г- О уравнение (6.57) совпадает с (5.37), если заменить

i sin со/ на bi и р sin (ш/-Ь Ф) на bv. Предлагаем читателю самостоятельно пояснить этот результат.