где (хо, Х20) определяет начальные условия и / (е) - релейная характеристика с зоной нечувствительности:

1, е>2;

ы=/{е) = j О, е2;

-1. е<-2.

Можно показать, что эта система асимптотически управляема, т. е. и (t)

(10.13)

О при i-> 00 *.

Однако коэффициент затухания выходного сигнала линейного элемента а О, и, следовательно, условия леммы 10.2 не выполняются. Действительно, в рассматриваемой системе выходной сигнал асимптотически не убывает, так как зона нечувствительности нелинейного элемента Б присутствии интеграторов позволяет выходному сигналу - е (t) принять любое значение внутри зоны нечувствительности - 2 е (оо) 2, зависящее от начальных условий.

Доказательство леммы 10.2. Прежде всего рассмотрим случай а = 0. Из выражения (10.1а) следует, что

е(01ео(0 +

g{t - х)и (т) dt

(10.14)

Ввиду неравенств (10.9) и (10.10) при а = О можно воспользоваться теоремой Парсеваля** для интеграла свертки в выражении (10.14), которая дает

g{t - x)u{x)dx

Принимая во внимание неравенство (10.9), имеем

G(/co) \gii)\dt<oo.

(10.16)

Используя соотношения (10.15), (10.16) и неравенство Минковского из выражения (10.14) получим

]e{i)dt] (]el{t)dt

\0 J \0

I G(/co)pt/(/co)Mco

elit)dt

(10.17)

g(t)\dt \ ut)dt у <оо.

С учетом неравенств (10.9) и (10.10) все члены в правой части неравенства (10.17) ограничены; таким образом, условие (10.11) для а = О выполняется и, следовательно, лемма для этого случая доказана. Для того чтобы доказать лемму для произвольного а, положим

u{t) = e*u{t); ea{t) = e *e{f). ] Подставляя эти выражения в выражение (10.14), найдем

(10.18)

\gait - )Ua{i)dx

* Асимптотическое поведение такой системы можно исследовать, например, методами фазовой плоскости. См. гл. 4, упражнение 4.17. ** См. приложение III. *** См. приложение III.

Поскольку все функции в этом неравенстве удовлетворяют условиям (10.9) и (10.10) при а = О, то для доказательства леммы следует вновь проследить выполнение соотношений (10.15)-(10.17).

Если для линейного элемента в дополнение к степени устойчивости а выполняется условие je {t) \ Мо ехр (-af), где Мо зависит от множества начальных условий, то неравенство (10.14) можно записать в виде

e-\g{t-x)e\{x)dx .

\e{t)\M--\-e

В последнем неравенстве подынтегральное выражение умножено и разделено на ехр (-а {t - т)).

Используя неравенство Шварца *, запишем

1(01

Мо +

\e-g\x)dx

\±. (

2 / f 2ат.,2

Л(Т)ЙТ

\ 1 1

/ J

Ме\

e *u\t)dt] <оо.

Поскольку М ограниченно, то ввиду условий леммы ограничен и выходной сигнал.

10.3. ОСНОВНАЯ ТЕОРЕМА И НЕКОТОРЫЕ ЕЕ ПРИМЕНЕНИЯ

Теорема 10.1 (теорема В. М. Попова). Рассмотрим систему с обратной связью (см. рис. 10.1), которая удовлетворяет уравнениям (10.1), и допустим, что выходной сигнал линейного элемента устойчив. Чтобы система имела абсолютно асимптотически устойчивые управление и выходной сигнал для (и/е) с [О,/С], достаточно, чтобы существовало такое действительное число q, что для всех действительных со О при произвольно малом б >> О выполняется следующее условие:

Re [(1 + М) G (/со)1 + -1- б > 0.

(10.19)

В зависимости от вида нелинейного элемента на параметры q я К накладываются следующие ограничения:

1) если и = f (е)- однозначная стационарная нелинейность, то

- оо <; 9 < при О <; /С < оо; О ! q <С оо при /С < оо;

2) если и = 1е (f)] - нелинейность с пассивным гистерезисом, то

О < /( < оо и -оо < <? 0;

3) если W = [е (i)] - нелинейность с активным гистерезисом, то

0</Соо и 09<оо;

4) если и]= [е (t), t] - обобщенная нелинейность, нестационарная и, возможно, с гистерезисом, то

0</Соо и q = 0.

* См. приложениеШ.

Если в случаях, указанных в пунктах 1), 2) и 4), /С = оо, то должно выполняться условие (10.3) *.

Доказательство теоремы (10.1) дано в приложении III. Указанная теорема является основной. Условия (10.19) теоремы (10,1) будем называть условиями Попова.

Заметим, что сформулированная теорема устанавливает взаимную связь требований, предъявляемых к линейному и нелинейному элементам.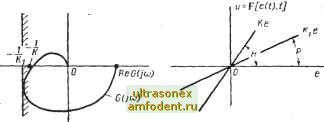

Рис. 10.3: а) Иллюстрация условия (10.19) для =0. Если годограф G (/со) лежит правее вертикальной прямой и все остальные условия теоремы 10.1 выполняются, то основная система с обратной связью имеет абсолютно асимптотически устойчивые управление и выходной сигнал для всех (и/е) £ 6 [О, K-i]; б) Допустимый (по Попову) сектор Р для расположения нелинейного элемента и (t) = [е (t), t], когда гарантируется абсолютная асимптотическая устойчивость управления и выходного сигнала

Например, для общего случая нелинейности, которая может быть нестационарной и проявлять гистерезисные свойства, мы должны в условиях (10.19) положить 9 = 0. Это определяет ограничения на расположение кривой G (/ш). Если нелинейная характеристика однозначна и стационарна, то возможная область размещения годографа G Ою) расширяется за счет выбора параметра q из возможного диапазона его изменения. В дальнейшем рассмотрим большое число различных связей.

Обратимся к геометрической интерпретации теоремы на основе амплитудно-фазовых характеристик. Рассмотрим простейший случай: q = 0. Тогда должно вьшолняться условие

ReG(/(o)> -для 9 = 0;

отсюда следует, что система характеризуется абсолютно асимптотически устойчивым управлением для (н/е) G [О, Кг], если годограф G (; ) лежит правее вертикальной линии, проходящей через точку (-UKi), как показано на рис. 10.3а. В соответствии с теоремой 10.1 условие q = Ь означает, что на выбор нелинейного элемента наложены минимальные ограничения. В этом случае наложены максимальные ограничения на выбор линейной части.

* Условие 6>0 в неравенстве (10.19) необходимо при доказательстве теоремы 10.1. Для практических целей неравенство (10.19) можно записать в виде

Re [(l + ;w9)G(yw)]+->0.