10.8. ПРИМЕНЕНИЕ НОМОГРАММ ЗАМЫКАНИЯ ПРИ ИСПОЛЬЗОВАНИИ КРИТЕРИЯ ПОПОВА

Метод проектирования линейных систем, связанный с применением номограмм замыкания, имеет значительные преимущества перед иными методами и широко распространен на практике. В этом параграфе воспользуемся им и для анализа систем на основе критерия Попова

Основное достоинство логарифмических амплитудных и фазовых характеристик перед частотными годографами заключается в простоте отыскания

arcigq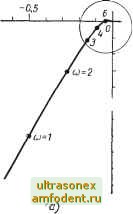

-0,15

--0,5

--1,0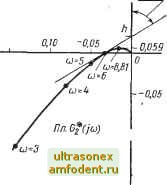

--0,10

--0,15

Рис. 10.18: а) Годограф Gj (/со) для примера 10.12; б) Конечный участок годографа

корректирующих цепей. Однако не надо забывать, что если использовать логарифмические характеристики G* (/со), то возникают трудности, связанные с тем, что модифицированное преобразование произведения передаточных функций не равно произведению модифицированных преобразований, т. е.

Gi (/со) 0-2 (/со)]* ф Gi (/со) GI (/со).

(10.39)

Поэтому предпочтительнее использовать логарифмические частотные характеристики исходного объекта G (/со).

1. Случай, когда 17 = 0. Допустим, исходная система имеет вид, показанный на pjHC. 10.19, а, где линейный элемент имеет передаточную функцию G (s), а нелинейность расположена в секторе (и/е) G Ы, Ь]. Рассмотрим преобразование сдвига полюсов вида

Uk{t) = U{t)-

e{t), b>a;

(10.40)

это преобразование приводит к тому, что

0(Р)

Gk{p) =

-G(p)

(10.41)

1 См. работу [142].

Однако в дальнейшем мы будем использовать и логарифмические характеристики модифицированной передаточной функции G* (/со) при q ф 0.

и реакция на начальные условия равна

l+G(s)

(10.42)

Характеристика нелинейного элемента после указанного преобразования должна располагаться в секторе

ifc Г Ь - а b - al (10.43)

, По теореме (10.4) область допустимого расположения частотной характеристики исходного элемента на плоскости G (/со) расположена вне области критического круга и вьщелена штриховкой на рис. 10.19, а. Назовем эту область областью Попова.

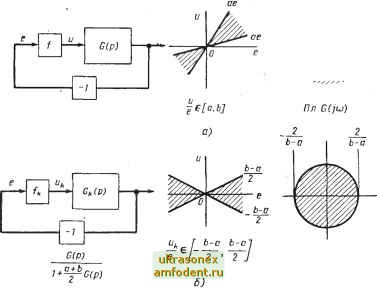Рис. 10.19. Преобразование сдвига полюсов вида (10.40): а - для системы с передаточной функцией С (s) н нелинейностью f, расположенной в секторе {и/е) [с, Ь ] (О < й < Ь < со); б - блок-схема системы, полученной в результате преобразования (10.40)

Преобразование (10.41) переводит указанную область Попова во вну-

тренность круга с центром в начале координат и р,адиусом-jzr плоскости

Од, (/со)>, что иллюстрируется на рис. 10.19, б. Следовательно, всякая окружность радиуса G, (/со) преобразуется в окружность на плоскость G (/со). Это преобразование аналогично тому, которое устанавливает связь между частотными характеристиками замкнутой и разомкнутой систем и может быть определено через номограмму замыкания.

) Этот результат приводит к следующей теореме (упражнение 10.5).

Основная система с обратной связью (см. рис. 10.1) с зависящим от времени коэффициентом усиления и = k (f) е и устойчивым выходом линейного элемента характеризуется абсолютно асимптотически устойчивыми управлением и выходным сигналом для k (t) < К, т. е. для (ule) £ [-К, К], если К \ G (/со) < 1.

Эта теорема близка к теореме, доказанной Д. Бонжорно [24 ] несколько иным способом.

Номограммой замыкания будем называть диаграмму, на которой в координатах 20 log I z\ (дб) и arg z (град), где z - исходная неременная, изображаются кривые постоянной амплитуды -j-qrj фазы arg уф- Нас

интересуют лишь кривые постоянной амплитуды

. Таким образом, 2

задача заключается в том, чтобы изобразить кривые G/j (/со) [ = -- -

в функции исходной передаточной функции G (/со).

Согласно соотношению (10.41) можно получить кривые

G (/ш)

огдбЦи) (град) -180

6 -о

(10.44)

Используя уравнение (10.44), можно построить критические окружности и, следовательно, границы области Попова, а с помощью номограмм замыкания -

ЬА-а

кривые постоянных амплитуд

Ь - а

Рис. 10.20. Номограмма, определяю-

, Ь-\-а Ь+а щая зависимость 20Ig - от --

G Ош)

в функции амплитуды и фазы переменной Г- G(/co). Эти кривые построе-

6.-fa

ны на рис. 10.20. Кривые постоянных значений -£5 > вьфаженные в децибелах, соответствуют кривым постоянного усиления замкнутой системы на номограмме замыкания.

Круговой критерий теоремы 10.4 будет выполняться для заданных

значений а и b п q = О, если годограф G (/со) лежит вне области, огра-

Ь + а Ь - а

ничейной кривой постоянного уровня 20 log

. Справедливо и обрат-

ное утверждение, показывающее, что значения а и 6, которые соответствуют

максимуму 20 Ig и для которых эти кривые касаются годографа

G (/со), определяют границы сектора Попова (ule) [а, Ь] для данной

задачи. Последнее утверждение чрезвычайно полезно использовать при отыскании допустимых секторов Попова. Покажем это на примере.

Пример 10.3. Проанализируем асимптотическое поведение линейной нестационарной системы, описываемой уравнением

(О + 2ё (О -I- (с - 3 - d cos сооО е (О = 0. (10.45)

Это уравнение является уравнением Матье * с демпфирующим членом. Для его исследования методами данной главы составим по уравнению (10.45) структурную схему (см. рис. 10.21),

где ,

(ule) е [а, Ь] = [с - d, с -f d]; G (р) = - - 1) (р + 3)

Линейный элемент характеризуется устойчивым выходом, только при охвате его отрицательной обратной связью с коэффициентом Л> 3. Таким образом, для выполнения круго-

* См. работу [137].