где корни характеристического квадратного уравнения имеют

вид:

i., = -l(t]±l/tl + e). (4-125)

В формуле (4-125) введеноспециальное обозначение для относительной толщины базы

: L-

у бездрейфовых транзисторов этот параметр определяет величину коэффициента переноса х [см. (4-18)].

Теперь запишем граничные условия, с помощью которых можно найти коэффициенты и Л..

Первое граничное условие можно основать на том, что полный дырочный ток при л: = О равен сумме диффузионной и дрейфовой составляющих. Используя выражения (1т72а) и (1-73а), учитывая соотношение (1-74) и подставляя значение Е из (4-121), получаем:

В качестве второго граничного условия примем .- .

р(ш) = 0.; (4-1266)

оно соответствует значению \UJ > фт- в общем выражении (4-166).

Используя корни (4-125) и найдя коэффициенты и Лг с помощью граничных условий (4-126), можно представить стационарное распределение концентрации в следующем общем виде:

sh

qDS r)shKr)2+£2+j/2+2chKr)2+g2 (4-127a)

В случае однородной базы (г] = 0) выражение (4-127а), естественно, переходит в (4-176). При дополнительном условии t, 1 получаем почти линейное распределение (4-17в). Этому распределений) на рис. 4-40 соответствует кривая с параметром т) = 0.

Если пренебречь рекомбинацией в базе, т. е. положить С - О, то распределение приобретает.существенно более простой вид :

hpw 1-е V У

* в случае однородной базы, для которой т) = О, корни имеют значения Si.g=d: При этом выраясенке (4-124) переходит в выражение (4-15) с точностью до члена ро. опущенного в уравнекик (4-122).

-Формулу (4-1276) можно получить непосредственно из (4-127а) либо пола-Гая 1,==оо в исходном уравнении (4-122), либо используя корни (4-125), которые npK.g=:Q имеют значения %x==.2\\lw и 2г=0.

Первый множитель в выражениях (4-127) есть граничная концентрация неосновных носителей для бездрейфового транзистора с тонкой базой [см. (4-17в) при х = 0]. Эта концентрация выбрана в качестве основы масштаба на рис. 4-40 и обозначена через

PD (0).

- Из выражений (4-127) следует, что граничная концентрация у дрейфового транзистора всегда меньше, чем у бездрейфового: р(0)<рд(0).

Режим высокого уровня инжекции имеет у. дрейфовых транзисторов свою специфику, которая состоит в следующем. Поскольку

равновесная концентрация основных носителей спадает вдоль оси X весьма резко (экспоненциально), а концентрация избыточных неосновных носителей Др меняется сравнительно слабо (см. рис. 4-40), то уровень инжекции Ар/По оказывается максимальным не на эмиттерной границе базы (как у бездрейфовых транзисторов), а вблизи коллектора (см. рис. 4-39). Отсюда следует, что с увеличением тока модуляция удельного сопротивления-базы (см. § 2-8) происходит в направлении от коллектора к эмиттеру и что приэмит-терный слой базы модулируется слабее других. Поэтому коэффициент б в выражении (2-69), характеризующий пр и-эмиттерный уровень инжекции, у дрейфовых транзисторов редко превышает единицу даже при больших токах, тогда как у транзисторов с однородной базой значение б достигает 10-100. Соответственно коэффициент инжекции [см. выражение (2-74)] у дрейфовых транзисторов зависит от тока сравнительно слабо.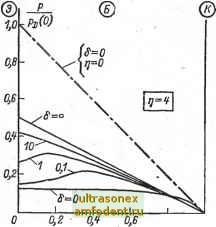

0,8 x/iu

Рис. 4-41. Распределение неосновных носителей в базе дрейфового транзистора при высоких уровнях инжекции (штрих-пунктиром показано распределение в бездрейфовом транзисторе при низком уровне инжекции).

Распределение инжектированных носителей при высоком уровне инжек-VfiK (рис. 4-41) [65] можно пояснить, исходя из, следующих соображений. Как известно, модуляция удельного сопротивления базы связана с ростом концентрации, о с н о в н ы X носителей, в нашем случае - электронов. Вблизи коллектора, где модуляция максимальна (см. выше), концентрация электронов намного превышает равновесное значение. В результате распределение электронов на модулированном участке оказывается более равномерным, чем в равновесном состоянии, а собственное электрическое поле соответственно более слабым. Иначе говоря, модулированный участок в значительной мере лишен дрейфовой специфики

и подобен базе бездрейфового транзистора. В частности, на этом участке распределение дырок должно быть почти линейным

Все сказанное подтверждается кривыми на рис. 4-41. Рассмотрим типичную кривую с параметром S = 0,1. Ее начальный участок почти горизонтален, поскольку здесь модуляция несущественна и дырки движутся в основном за счет дрейфа в собственном поле базы. Конечный участок кривой почти линеен, поскольку здесь модуляция максимальная, собственное поле практически отсутствует и дырки движутся под действием градиента концентрации с удвоенным коэффициентом диффузии [см. (2-72)]. Промежуточный участок характерен повышенной концентрацией дырок, поскольку в направлении от начального участка к конечному собственное поле убывает, а значит, уменьшается скорость носителей и происходит их накопление. Разумеется, повышенная концентрация р должна быть достаточной для того, чтобы дрейфовая составляющая тока могла пере компенсировать диффузионную составляющую, обусловленную положительным градиентом концентрации на этом участке.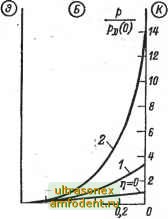

Если дрейфовый тран.зистор работает в инверсном включении, то главная специфика состоит в том, что собственное поле Е препятствует движению носителей, инжектированных через коллекторный переход. С аналитической точки зрения в уравнении (4-122) изменится знак второго члена, а в результирующих выражениях (4-127) коэффициент т] следует считать отрицательным. Соответственно распределение р (х) без учета рекомбинации (4-1276) принимает вид:

a:/w0,8 0,Б 0,4

Рис. 4-42. Распределение концентрации инжектированных дырок в базе дрейфового транзистора при инверсном включении.

(4-128)

где координата х отсчитывается от коллектора к эмиттеру.

Кривые р (х) для инверсного включения показаны на рис. 4-42. Как видим, они существенно отличаются от кривых р {х) для нор-

Напомним, что в транзисторе с однородной базой диффузионный ток при высоком уровне инжекции составляет лишь половину полного тока [см. (2-72) к рис. 2-36, б]. Поэтому на рис. 4-41 асимптотическая прямая с параметром о == оо (общая для дрейфовых и бездрейфовых транзисторов) имеет вдвое меньший накло1Г, чем штрихпуиктирная прямая с параметром 6=0, соответствующая транзистору с однородной базой. Общность асимптотической Рямой fi=oo для однородной и неоднородной баз обусловлена следующим: если концентрации избыточных носителей намного превышают концентрации равновесных, то характер распределения последних (а значит, и характер распределения примеси в базе) не оказывает существенного влияния на распределе-ие избыточных носителей, и это распределение оказывается одинаксжым в транзисторах с однородной и неоднородной базами.