тическое значение Ер (см. табл. 1-1), то подвижность -

fx = M-o(%-) . (1-34)

где Е > Ещ, а Но - подвижность при Е = Режим Е > fsp носит название сверхкритического.

Критическая напряженность поля не является строго определенной величиной; она лишь приблизительно соответствует условию, ~ когда направленная (дрейфовая) скорость носителей делается сравнимой с их хаотической (тепловой) скоростью, например ц£кр = 0,lvr, Однако даже такое приближенное условие позволяет констатировать, что критическая напряженность, учитывая (1-27), (1-32) и (1-33), является функцией температуры (Гкр 7+ /), концентрации {EpyN) и начальной подвижности (f I/H-o)- Последняя зависимость, в частности, объясняет меньшие значения у германия по сравнению с кремнием.

Сравнимые значения дрейфовой и тепловой скоростей позволяют говорить о том, что суммарная скорость носителей в сверхкритическом режиме повышается, а значит, их температура оказывается соответственно выше окружающей. Носители с повышенной температурой, т. е. с энергией, сравнимой или превышающей тепло-

вую энергию 2 называют горячмим .

Горячие носители, взаимодействуя (сталкиваясь) с имеющимися акустическими фононами, сами подогревают решетку, порождая новые, более энергичные оптические фононы (см. сноску на с. 8). Порождение оптических фононов 110] приводит к новому явлению - насыщению скорости. А именно, при достаточно сильных полях [обычно при £ (4 -7-5) кр] скорость носителей перестает зависеть от напряженности поля; т. е. получается условие V - [iE = const.

Такой результат равносилен соотношению ц ~ Е~ вместо соотношения \i ~ ЕГ, лежащего в основе (1-34). Таким образом, полупроводникам свойственно понятие максимальной скорости носителей у акс- Эта скорость соответствует энергии №о.ф. необхо--димой для возбуждения опти.ческого фонона. Как только носитель в интервале между столкновениями накопит энергию Шо,ф и скорость у акс. он тотчас же теряет их на образование оптического фонона и опять начинает разгоняться с нуля . Поэтому значение

макс можно оценить из элементарного соотношения/ *У= о.ф. где энергия Wo, как показывает теория, близка к тепловой энергии холодной решетки--AT. Получающееся значение у акс при-

* Поскольку энергия кТ характеризуется температурным потенциалом (1-3), который при 7 =300 К составляет около 25 мВ, можно считать, что при комнатной температуре горячими являются носители с энергией 0,03 эВ и выше.

мерно составляет 10 см/с. Более точные значения приведены в табл. 1-1.

Зависимость ц (Е) оказывает непосредственное влияние на вольт-амперную характеристику полупроводника. Например, в простейшем случае (однородный кристаллспостоянным сечением)

ток / пропорционален скорости v, а напряжение U - напряженности электрического поля Е, поэтому форма кривой / {U) такая же, как кривой V (£) (рис. 1-20)*. На начальном участке соблюдается закон Ома, поскольку \х = const и, следовательно, v Е. На последующих двух участках этот закон все больше нарушается, вплоть до насыщения тока. Значит, при достаточно больших напряжениях (когда поле Е > £кр) полупроюдник ведет себя как нелинейный резистор.

ЛЗмаческшк участок

10 . 10 Енр 10 В/см

Рис. 1-20. Зависимость скорости носителей от напряженности электрического поля.

1-9. УДЕЛЬНАЯ ПРОВОДИГЛОСТЬ И УДЕЛЬНОЕ СОПРОТИВЛЕНИЕ

В общем виде удельная проводимость выражается следующим образом h

о=- = № + дар. (1-35)

где \1п, Ир - подвижности электронов и дырок; р - удельное сопротивление.

* Действительно, при постоянном сечении и постоянном удельном сопротивлении значение U определяется элементарным соотношением U=EWf где W - длина образца. Что касается значения /, то оно (при постоянном сечении) пропорционально плотности тока, определяемой соотношением

const

где % - концентрация подвижных зарядов. В однородном кристалле К -и, следовательно, / - v.

Это и последующие выражения основаны на соотношении для плотности тока, приведенном в предыдущей сноске. В самом деле, учитыиая два типа носителей, можно записать:

где % = qn и кр= qp. Подставляя ti = х £ и tip=Ap£ и сравнивая полученное выражение с дифференциальной формой закона Ома (/= оЕ), приходим к формуле (1-35) и ее частным случаям.

Для частных случаев собственного, электронного и дырочного полупроводников получаем соответственно:

Oi = = дщ{\1п + \1рУ, о = я qnii ;

{1-36а) (1-366) (1-Збв)

Если в формуле (1-35) концентрацию р выразить через п с помощью соотношения (1-16), то, как легко убедиться путем дифференцирования, минимальное значение удельной проводимости

Омин=29Пг1ц Ир (1-37)

получается при концентрациях

n=nilYb\ р=тУь,

где b - отношение подвижностей (1-31). Сравнивая (1-37) и (1-36а), нетрудно показать, что 0 н < сг;, т. е. минимальная удельная проводимость свойственна не собственному, а слегка примесному по.чупроводнику. Если Ь > 1 (как обычно и бывает), то значение а ин соответствует дырочной проводимости. Для германия и кремния значение а ин на 7 и 12% соответственно меньше, чем Oj.

Температурную зависимость удельной проводимости или удельного сопротивления можно получить, зная температурную зависимость концентрации носителей (§ 1-7) и их подвижности (§ 1-8).

В широком температурном диапазоне зависимость о(Т) удобно изображать в полулогарифмическом масштабе, откладывая по оси абсцисс обратную температуру 1/Г (рис. 1-21). В этом случае для собственного полупроводника получается прямая, наклон которой пропорционален 0,5 фз. Этот результат следует из выражения (1-36а), если подставить в него (1-15) и (1-32).

Для примесных полупроводников зависимость с (Г) получается сложнее. В области очень низких температур (большие

значения 1/7, когда степень ионизации примеси мала, получается прямая с наклоном, пропорциональным 0,5 фсд или 0,5 фа * Так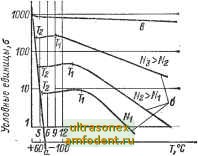

Рис. 1-21. Зависимость удельной проводимости по.чупроводника от температуры.

а - собственный полупроводник; б - примесные полупроводники; в - полуме-

* Действительно, если, например, уровни доноров почти все зетолшпы, то совокупность этих уровней образует своего рода валентную зону, отделенную от зоны проводимости расстоянием фд. Последнее играет роль ширины запрещенной зоны, и вместо наклона 0,5 фз получается наклон 0,5 ф.