Из выражений (8-28а) и (8-286) следует, что входное и выходное сопротивления под действием обратной связи существенно уменьшаются; это характерно для данного типа обратной связи. Практически при токе /э = 1 -мА входное сопротивление составляет 100- 300 Ом, а выходное - около 1 кОм.

Частотные и переходные характеристики коэффициента усиления каскада можно оценить, подставляя изображение (7-39) в (8-29а). После преобразований получим:

где Ки о.с выражается формулой (8-29а), а постоянная времени

Используя формулы (7-41), (7-36) и (7-16) и полагая >> б + + г нетрудно представить постоянную времени в виде

(Тв)о. с -Щ [ta + С, {RMl (8-316)

В области низших частот пониженные значения R ухудшают частотные свойства и заставляют использовать большие переходные емкости.

Общая обратная связь. Общая обратная связь выгоднее местной при том же коэффициенте усиления. Проиллюстрируем это важное положение.

Пусть имеется Л/-каскадный усилитель с коэффициентом усиления Aq = А, где Ах - усиление одного каскада. Рассмотрим два случая:

1) вводится общая обратная связь с глубиной 1 + Ио/4ц;

2) вводится местная обратная связь в каждом каскаде с глубиной 1 + щА. Примем, что результирующий коэффициент усиления в обоих случаях

одинаков, тогда

А А, \N

\\+щА,)

Взяв производную dAo.c/dA( нетрудно получить выражение тина (8-2) для относительной нестабильности в случае общей обратной связи:

dA 1

общ Ао 1+щАо

Аналогично, взяв производную dAg.JdAi, получим относительную нестабильность при местной обратной связи:

dAi N

Оместн- Г

dA .c

местн Al l+KiAi

Из исходного равенства А = А находим: dA(,/A(, = Л (dAi/Ai), а из выражения для Ао.с (см. выше) следует: I + к(,А(, = (I + tciAi). С учетем обоих соотношений запишем искомую связь в следующем виде:

Дрбвд 1 1

(1-fMi)- (1-fMo)

Отсюда ясно, что бобщ < MecTHt причем для глубокой обратной связи разнкца может быть весьма значительной. Например, если /V = 2 и 1 + > Но = 25, то 6 o6ui= 0,26м£стн- С ростом числа каскадов выигрыш увеличивается.

Как известно [62], использование общей обратной связи в усилителях с числом каскадов больше трех обычно приводит к самовозбуждению или во всяком случае должно сопровозкдаться специальными мерами стабилизации. Поэтому рассмотрим только случаи двух- и трехкаскадкых усилителей.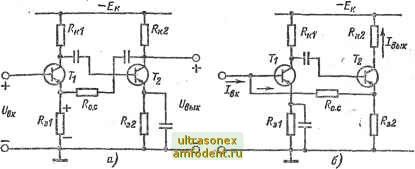

Рис. 8-7. Двухкаскадные усилители с общей обратной связью. а - последовательной по напряжению; б - параллельной по току.

Схема обратной связи, как обычно, выбирается, исходя из назначения усилителя, т. е. в зависимости от характера входной и выходной величин (ток или напряжение), а также от желательного изменения в ту или иную сторону входного и выходного сопротивле-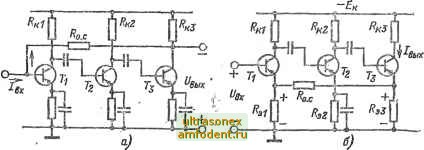

Рис 8-8. Трехкаскадные усилители с общей обратной связью. а - параллельной по напряжению; б - последовательной по току.

НИИ. На рис. 8-7 показаны два типичных варианта обратной связи в двухкаскадных усилителях, а на рис. 8-8 - в трехкаскадных.

Если сравнить анализ такого рода схем с анализом рассмотренных выше однокаскадных усилителей, то окажется, что он сложнее в части переходных и частотных характеристик, а также вопросов стабильности, но проще в области средних частот. Последнее объясняется тем, что в многокаскадных усилителях цепь прямой

передачи характеризуется таким высоким значением коэффициентя передачи Л, при котором глубокая обратная связь обеспечивается при весьма малых значениях коэффициента . обратной связи к. Малые значения х способствуют однонаправленности цепи обратной связи, а также слабому влиянию ее входных и выходных параметров на коэффициенты и ых- Кроме того, большие значения Л позволяют считать практически неизменной входную величину цепи прямой передачи (см. на рис. 8-1).

Все эти особенности существенно облегчают расчеты, тем более, что в области средних частот коэффициент передачи при глубокой обратной связи выражается элементарной формулой (8-3).

В схеме на рис. 8-7, а (которую часто называют двойкой ) действует последовательная обратная связь по напряжению. Значит, усилительным параметром согласно рис. 8-2, а целесообразно считать коэффициент усиления Ки-

В общем случае, как следует из табл. 8-1,

Коэффициент Ки рассчитывается по формуле (7-58а). Полагая Рое = Р; < Rbxi ~ Pi/?si и R,a > /?вх2, получаем:

Если А/д]. < А/о.с (что обычно выполняется), то и есть коэффициент передачи делителя Ri - Ro c, т. е.

Э1 + О.С

Следовательно, при глубокой обратной связи выражение (8-32а) переходит в следующее:

Условие i?o.c Rai, при котором Ки о.с U лсгко выполнимо: оно не противоречит условию глубокой обратной связи (}с Ка 1) благодаря большому усилению Ки- Типичными значениями явля-кугся: Ка = 500 2000; R = 5+10 кОм; R = 50н-200 Ом; при этом 1 -f ХаКи = 20+50 и Ки о.с = 25-ь40.

Глубокая обратная связь и высокая устойчивость делают дант ную схему удобным элементом линейных импульсных усилителей 1123].

Строго говоря, в схеме действует двухпетлевая обратная связь: общая по напряжению и местная ( в 1-м каскаде) по току. Если представить выход цепи X так, как показано на рис. 8-2, в, то резистор JRgi можно отнести к цепи прямой передачи. Тогда усиление и входное сопротивление 1-го каскада можно рассчитывать по формулам (8-21) и (8-19).