с помощью (2-33) это распределение легко записать следующим образом:

Ар(л;; 0) = ро-/е - (2-S9)

Изображением производной -- будет s [Ар - Ар (л:; 0)],

и диффузионное уравнение (1-79а) в операторной форме приводится к виду

i!jf i+ilAp = .Ap(;,;0). (2-100)

Частным решением уравнения является функция Др = Др {х; 0): это легко проверить подстановкой выражения (2-99). Общее решение имеет прежний вид (2-90). Исходя из граничных условий

= -/2:

Др(оо) = 0,

после преобразований получим изображение избыточной концентрации:

Др(л:; s) = po

По таблицам находим оригинал этой функции для л: = 0:

(2-101)

Др(0; Щ = Ро{1

(2-102)

Приравняв (2-102) и (2-28а), легко найти напряжение на переходе (рис. 2-42, б):

ы(e) = фrln(l-f А А+/?.егГ1/ ё ). (2-103)

Время рассасывания бр обычно определяют, полагая V (Эр) = О, т. е. считая, что этап рассасывания заканчивается тогда, когда граничная концентрация носителей достигает равновесного значения. При этом время бр получается в неявном виде:

Используя аппроксимацию (2-93а), можно получить время бр в явном виде:

Например, если 4 = h, то бр 0,3. С увеличением запирающего тока /а время рассасывания уменьшается, что вполне естественно.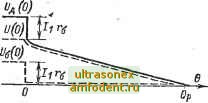

Рис. 2-43. Этап рассасывания при вы-к.чючении.

Полное напряжение на диоде в момент бр равно -ITf, (рис. 2-42, б). Значение в первом приближении можно рассчитать по формуле (2-77а), поскольку за время бр заряд дырок в базе меняется незначительно (см. рис. 2-42, а). До переключения ка базе падало напряжение Ч-б- Поэтому в момент переключения диода получается так называемый омический скачок напряжения:

ДгУд = АС/б = -(/1-Ь/2)Гб.

Теперь рассмотрим случай, когда /2 = О, т. е. когда диод не переключается, а отключается (см. рис. 2-40, правая часть). В момент отключения омический скачок напряжения равен - hr, после чего напряжение Le остается равным нулю, так как /2 = 0. Следовательно, после отключения имеем U

и напряжение на переходе согласно (2-103) меняется следующим образом (рис. 2-43):

ы(е) = фНпГ1 + т O-erf (2-105)

L о J

Если в квадратных скобках выделить множитель 1 -f- /j/Zo и прологарифмировать полученное произведение, то выражение (2-105) можно привести к виду

ы(е)={У(0) + ф7-1п(1-erf]/9), (2-106а)

где для простоты множитель /,/(/о + /1) при erfl/e положен равным единице. Применяя аппроксимацию (2-93а), получаем переходную характеристику в форме, удобной для построения и анализа:

ы(е)==/(0)-Ьфг1п(1-]/ (2-1066)

В начале переходного процесса, когда 9 < 0,5, можно восполмоваться аппроксимацией (2-936) и разложить логарифм в ряд, ограничиваясь членом первого порядка; тогда

к (6) и г/ (0)-(pj-Vf. (2-1 of а)

При достаточно больших значениях 9 используем аппроксимацию (2-93в) и получаем линейную характеристику:

иф)и (0) - ф (6+In 2). (2-1076)

В самом конце процесса, когда второе слагаемое в квадратных скобках выражения (2-105) меньше единицы, разлагая логарифм в ряд и используя после этого аппроксимацию (2-93в), получаем экспоненциальный участок характеристики:

и(9) =4е-в- (2-107В)

Нй этом участке напряжение U не превышает долей ф, т. е. пренебрежимо мало. Поэтому основным участком характеристики является линейный.

Из формулы (2-1076) можно оценить время рассасывания, полагая L/ (Эр) - О и пренебрегая слагаемым In 2 (это дает (некоторый запас , учитывающий часть экспоненциального хвоста ):

Лп. (2-108)

U(0)

Например, если IJI = 1№, то бр П. Как видим, время рассасывания в случае выключения несравненно больше, чем в случае переключения (даже если последнее осуществляется сравнительно небольшими обратными токами /г).

Восстановление обратного тока (сопротивления). Этот участок переходной характеристики (рис. 2-44) наиболее сложен для анализа. Строгое решение [461 дает три разных закона изменения тока в трех смежных интервалах времени, что, конечно,

крайне неудобно на практике. п

Рис. 2-44. Зтап восстановления обрат-

Приводимое ниже решение ис- - обратного напряжения, ходит из вполне оправданного допущения о том, что в начале рассматриваемого участка (при / = 0) распределение дырок в базе вырщкается разностью двух экспонент ;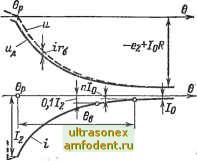

Ар (л; 0)=ро

(2-109)

где г < L.

Функция (2-109) ргвна нулю при л: = О и при л: = схз и имеет максимум между л: = О и л: = L, что соответствует физической картине процессов в толстой базе в конце стадии рассасывания (см. кривую на рис. 2-42, а). Эквивалентную длину / определим, исходя из граничного условия

а (Ар)

л;=0

куда подставим производную от концентрации (2-109). Вычисления приводят

к следующему результату: / = L-.-г-г-.

i + i

Из соотношения I < L следует, что вторая экспонента в выражении (2-109) уменьшается с ростом х быстрее, чем первая, значит, вдали от перехода распределение дырок близко к тому, которое было при прямом токе /i до переключения. Это также представляется физически справедливым.

Опуская несколько громоздкие выкладки, связанные с решением диффузионного уравнения (2-100), заметим лишь, что уда-

* Такая аппроксимация пг>и x-G дает Ар=0 вместо Ар=-ро. Эта Погрешность практически не сказывается на резульгатах.