Обычно к полупроводниковым материалам относят вещества, которые при комнатной температуре имеют удельное электрическое сопротивление р в пределах от -10 до 10-10 Ом-см *. Вещества со значительно меньшим сопротивлением (10 - 10 * Ом-см) причисляют к проводникам (металлам), а со значительно большим (10 -10 Ом см) -к непроводникам (диэлектрикам). Металлы и диэлектрики являются полюсами наиболее общего класса веществ - полупроводников. Количество полупроводниковых материалов, известных в настоящее время, далеко превышает число металлов и диэлектриков. К полупроводникам относятся некоторые химические элементы (S1, Ge, Se), интерметаллические соединения (InSb, GaAs), окислы (CugO, ZnO), сульфиды (CdS, ZnS), карбиды (SiC) и множество других химических соединений.

Различие между диэлектриками и полупроводниками в основном количественное. Различие же между металлами и полупроводниками отнюдь не сводится к различию удельных сопротивлений.

В отличие от чистых металлов сопротивление чистых полу-проюдников сильно зависит от температуры и, кроме того, с ростом температуры не увеличивается, а уменьшается. Так, для большинства металлов температурный коэффициент сопротивления составляет + (0,4-0,6) % на ГС, а для полупроводников он можег достигать - (5-6) % на ГС и более.

При добавлении примеси в чистый металл удельное сопротивление образующегося сплава (нихрома, манганина и т. п.) больше удельного сопротивления каждого из компонентов, тогда как при добавлении примеси в чистый полупроводник его удельное сопротивление сильно уменьшается: например, 10 % мышьяка в германии снижает сопротивление последнего в 200 раз.

Причины отмеченных особенностей полупроводников станут ясны после изучения их структуры и механизма проводимости.

* В полупроводниковой технике принято измерять удельное сопротивление для 1 см материала (1 Ом-см= 10 Ом-мм/м).

в дальнейшем будут рассматриваться главным образом кремний и германий - основные материалы, используемые в современной транзисторной технике. Однако закономерности, характерные для этих материалов, распространяются в общем на весь класс электронных полупроводншчов, в которых электрический ток обусловлен только электронами, а не ионами 11, 2].

1-2. СТРУКТУРА ПОЛУПРОВОДНИКОВ и типы птоводимости

Полупроводники представляют собой кристаллы, которые можно разбить на множество повторяющихся однотипных элементарных ячеек . Такие ячейки - структурные молекулы кристалла - подобно химическим молекулам состоят из нескольких атомов [3, 4].

Кристаллическая решетка кремния называется тетраэдриче-ской или решеткой типа алмаза. Она характерна также для германия и всех четырехвалентных элементов. В основе такой решетки лежит пространственная фигура - тетраэдр, в углах и центре которой расположены атомы (рис. 1-1. а). Характерная особенность тетраэдрической системы заключается в одинаковом расстоянии центрального атома от четырех угловых. Каждый угловой атом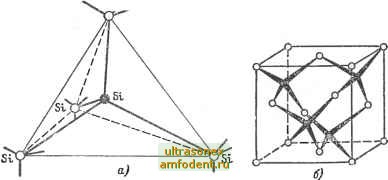

Рис. 1-1. Тетраэдрическая структура кристаллической решетки, а - элементарный тетраэдр; б - элементарная ячейка.

в свою очередь служит центральным для других четырех ближайших атомов. Совокупность нескольких тетраэдров образует элементарную ячейку (рис. 1-1, б) кубической формы с размером ребра около 0,5 нм (постоянная решетки).

Говоря о кристаллах, обычно подразумевают монокристаллы, которые в отличие от поликристаллов совершенно однородны, т е. обладают идеально!!, регулярной решеткой. Поликристаллы, несмотря на внешнюю однородность, имеют зернистую структуру, т. е. состоят из множества ыикрокристал-лов, разделенных межкристаллическими гранями, равносильными дефектам решетки. Для изготовления обычных полупроводниковых приборов (диодов, транзисторов) поликристаллы непригодны.

Всем кристаллам, в том числе типичным полупроводникам, свойственна анизотропия - зависимость свойств от направления, в котором эти свойства рассматриваются. Анизотропия является естественным следствием того, что пасстояния между смежными атомами различны в разных направлениях. Плоскости, лежащие внутри кристалла, и его наружные ррани принято обозначать индексами Миллера [4] - совокупностью трех цифр, характеризующих ориентацию плоскости относительно атомов элементарной ячейки. Так, применительно к кубической решетке индекс (100) соответствует плоскости, проходящей через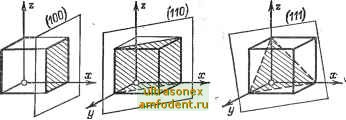

Рис. 1-2. Характеристические плоскости кубической решетки.

грань куба; индекс (ПО) - плоскости, проходящей через диагонали противоположных граней; а ивдекс (111) - плоскости, проходящей через три вершины, не связанные общими ребрами (рис. 1-2) Направления, перпендикулярные указанным плоскостям, обозначаются теми же индексами, но в квадратных скобках. Наиболее густым по числу атомов на единицу длины является направление [111], наиболее разреженным - направление [100].

В последующих выводах мы будем пользоваться плоским эквивалентом тетраэдрической структуры (рис. 1-3), в котором сохранена главная особенность решетки типа алмаза - одинаковые расстояния между смежными атомами.

Связь атомов в рассматриваемой решетке устанавливается вследствие наличия специфических обменных сил, возникающих в результате попарного объединения валентных электронов. Эти силы отражены на рис. 1-3 сходящимися стрелками. Объединение электронов следует понимать так: пара электронов, обведенная на рис. 1-3 пунктиром, в равной степени принадлежит обоим соответствующим атомам или, образно говоря, поочередно примыкает то к одному, то к другому. Соответственно в среднем каждый атом обладает устойчивой восьмиэлектронной оболочкой. Такая связь атомов, при которой каждый из них остается нейтральным, называется парноэлектронной, ковалентной [2] или просто валентной в отличие от ионной связи, обусловленной электрическими силами и имеющей место, например, в решетке каменной соли Na+Cl~, где атомы ионизированы.

В общем виде индексы Миллера определяются следующим образом. Начало прямоугольной системы координат помещают в одном из узлов решетки; отрезки I, т, п, отсекаемые данной плоскостью на осях координат, измеряют в единицах постоянной решегки, обратные величины /i, т, приводят к общему наименьшему знаменателю, после чего знаменатель отбрасывают. Числители образуют индексы Миллера.