ft ) i. При холостом ходе {R - оо) или при работе данного каскада на другой аналогичный каскад {R = R > Rk)

Ku-l. (8-226)

Выражения (8-22) соответствуют общему выражению (8-3), характеризующему глубокую обратную связь, когда усилительный параметр почти не зависит от свойств цепи прямой передачи и определяется коэффициентом обратной связи (в данном случае Ks = = -Ro)-

В области низших частот действительны все формулы § 7-3, за исключением (7-306), в которой следует заменить на Rg. Большие значения Rq и Rx в каскаде с обратной связью позволяют соответственно уменьшить переходные и блокирующие емкости.

В области малых времен и высших частот данный каскад имеет лучшие переходные и частотные характеристики, чем обычный каскад ОЭ. Это следует из выражения (7-41), где Р е и выражаются формулами (7-20) и (7-36), а коэффициент больше, чем в обычном каскаде ОЭ. При типичном условии Ро Тб >> 1 получаем постоянную времени в области высших частот:

b = Tirfl +A + Ck{RkIR )1 (8-23)

1 + V*

Добротность каскада, как отмечалось в § 7-4, ниже, чем в отсутствие обратной связи, и для восстановления добротности используется корректирующая емкость Со (рис. 7-16).

Местная обратная связь по напряжению. Типичная схема каскада с такой связью показана на рис. 8-6, а. В данном случае, когда каскадуявляется промежуточным, сопротивление обратной связи принято включать между коллекторами; при этом сигнал обратной связи попадает через переходную емкость С на базу этого же транзистора. Такую схему можно использовать и в одиночном каскаде.

Наличие внутренней обратной связи (через Гд) наряду с внешней (через RoJ делает обратную связь в целом многопетлевой. Чтобы не усложнять анализа, будем учитывать влияние только внешней связи; влияние внутренней связи отражается в параметрах цепи прямой передачи. Так как в данном случае обратная связь параллельная по напряжению, то в качестве параметров выбираем входную и выходную проводимости, а также сопротивление передачи (см. табл. 8-1).

Сопротивление передачи - параметр, который в гл. 7 не использовался. Его можно получить либо непосредственно из определения R = (/вых/б).? =оо (воспользовавшись эквивалентной схемой на рис. 7-4), либо с помощью соотношений, приведенных

Для типичных значений /?к11н = 3 5 кОм сопротивление не должно нревышать 0,5 кОм, что всегда выполняется.

в табл. 8-2, исходя, например, из параметра /< . Умножая обе части (7-4а) на R, заменяя р на %е й полагая R, Ra-oo (условие, соответствующее идеальной обратной связи рассматриваемого типа), получаем:

п==-И/-к1?к). (8-24)

Цепь обратной передачи (резистор Ro.c на рис. 8-6, б) будет однонаправленной, если ток / определяется только (или в основном) напряжением (/вых (которое является входным для четырехполюсника обратной связи, см. сноску на с. 357). Для этого необходимо выполнить неравенство U << (/вых- Учитывая соотношения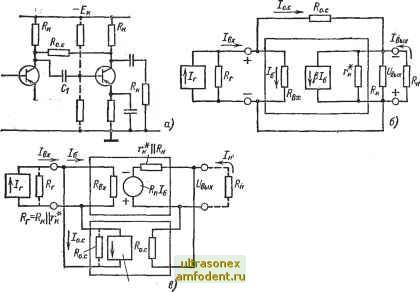

Рис. 8-6. Промежуточный каскад с местной параллельной обратной связью по напряжению.

а - принципиальная схема; б - эквивалентная схема; в - эквивалентная схема, приведенная к структуре на рис. 8-2, б.

Ur>. = hR..; t/вых - {rt II /?к II II Ro.d и /?в, < Р (г* II R, II /? ),

можно получить условие однонаправленности в следующем виде:

(8-25)

Поскольку выполнение этого неравенства не встречает затруднений, эквивалентную схему каскада (рис. 8-6, б) можно представить в канонической форме (рис. 8-6, е), которая соответствует общей структуре параллельной обратной связи по напряжению (рис. 8-2, б).

Параметрами однонаправленной цепи обратной связи будут:

R = -8o..\ (8-26а)

BXK = Bb,XK = go.C. (8-266)

Как известно, коэффициенты входа и выхода, существенно меньшие единицы, нетипичны и свидетельствуют о неудачно выбранном типе обратной связи (см. с. 363). Поэтому в дальнейшем положим 1вх - вык = I. т. е. будем считать сопротивления источника сигнала и нагрузки достаточно большими. Тогда глубину обратной связи можно записать в следующем виде:

1+K;j/? =1+P, Ао.с

а условие глубокой обратной связи - в виде

{rt\\RK)>Ro.c. (8-27)

Теперь, используя выражения, приведенные в табл. 8-1, нетрудно получить любой из основных параметров каскада с обратной связью. В случае глубокой обратной связи 1см. (8-27)] получаем:

(?Bx)o.c-f-; (8-28а)

(вых)о.с; (8-286)

> (? )о.с-о.с. (8-28B)

Запишем еще коэффициент усиления напряжения как более привычный параметр, чем R . Для этого, разумеется, нужно считать Rr конечной величиной. Подставим в выражение для (R )o.c (табл. 8-1) значения (?п)о.с = Ка ccRr и R = KaRc из табл. 8-2 и учтем соотношение (8-26а).

Тогда в общем случае

а при глубокой обратной связи

Р K o.c-f. (8-296)

Как видно из (8-296), с уменьшением сопротивления R коэффициент усиления возрастает. Однако одновременно согласно (8-29а) уменьшается глубина обратной связи, т. е. утрачиваются ее положительные свойства. При ij. О данный тип обратной связи лишен смысла.

Подставляя /?о.с из (8-296) в (8-27), получаем ограничение на коэффициент усиления в условиях глубокой обратной связи:

КСаКР-Ф. (8-30)

Например, если i? = г* R (т. е. если выходное сопротивление предыдущего каскада такое же, как у данного), то \Ки\ < Pi т. е. обычно не превышает 5-10.