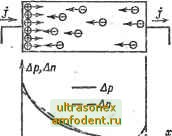Процесс, при котором диффундируют носители одного типа, а носители другого типа лишь обеспечивают квазинейтральность называют монополярной диффузией.

Несмотря на внешнее сходство в распределении носителей монополярная диффузия принципиально отличается от биполярной. Отличия состоят Б следующем.

1. Имеется результирующий ток; поэтому, в частности, полупроводник должен быть элементом замкнутой цепи Соответственно

помимо демберовского поля, сосредоточенного вблизи инжектирующей поверхности, во всей толще полупроводника действует обычное - омическое поле, обусловленное приложенным напряжением.

2. Потоки дырок и электронов направлены в разные стороны: дырки двигаются в глубь кристалла, а электроны - в сторону инжектирующей поверхности, в район электронно-дырочного облачка , где происходит интенсивная рекомбинация и необходимо пополнение основных носителей. Результирующий ток является суммой дырочной и электронной составляющих.

3. В связи с постоянством результирующего тока дырочная и электронная составляющие меняются в разные стороны: убывание дырочного тока от поверхности в глзбь кристалла сопровождается соответствующим ростом электронной составляющей. На самой инжектирующей поверхности электронный ток равен нулю, так как близко к нулю электрическое поле. Следовательно, в непосредственной близости от инжектирующей поверхности ток обусловлен только дырками. В глубине кристалла, где дырочный ток благодаря

рекомбинации делается равным нулю, обращается в нуль и диффузионная составляющая электронного тока. Следовательно, вдали от инжектирующей поверхности ток обусловлен только электронами и имеет чисто дрейфовый характер: электроны двигаются в омическом поле, созданном внешним напряжением.

Рис. 1-32. Монополярная диффузия в результате инжскции дырок в электронный полупроводник.

Указанные отличия принципиальны с физической точки зрения. С математической же точки зрения распределения Др (х) и Art (х) Ар (х) описываются либо уравнением биполярной диф фузии (1-102) (если полупроводник близок к собственному), либо (в случае электронного полупроводника) уравнением (1-78а).

Что касается выражения для поля Е, то оно в данном случае будет отличаться от (1-1006), поскольку результирующий ток не равен нулю. Подставляя (1-72) и (1-73) в (1-71), легко получить-

£ = 1

j + q(Dp-D )fl (1-108)

Сравнивая (1-108) с (1-1006), замечаем, что поле при монополярной диффузии складывается из постоянной (омической) и демберов-ской составляющих. В глубоких, квазиравновесных слоях, где dp/dx О, остается омическое поле Е = j/o в соответствии с выражением (1-104) для однородного полупроводника.

Строгое решение задачи о распределении носителей при моко-полярной диффузии затруднительно. Поэтому решим эту задачу для малых возмущений и в диффузионном приближении

Величину возмущения принято характеризовать уровнем ин-оюещии

g lip An

По По

т. е отношением концентрации избыточных носителей к равновесной концентрации основных носителей. Малому возмущению соответствует неравенство б 1, т. е.

Ap aiArt< o, (1-109)

которое называют условием низкого уровня инжекции. Это условие дает право пренебречь эффектом модуляции проводимости на возмущенном участке и принять в формуле (ЫОЗа) соотю пение о =к о Ор, характерное для равновесного электронного полупроводника. Следствием этого можно считать равенство - Dp

Диффузионное приближение характеризуется тем, что в уравнении (1-102) пренебрегают членом с £. С учетом этого пренебре->!<ения, а также условия = Dp уравнение (1-102) переходит в диффузионное уравнение (1-79а).

Поделив обе части (1-79а) на Dp, запишем нестационарный и стационарный варианты диффузионного уравнения в следующем виде:

-д-Ц Ц-дГ . (1-1Ша)

: = 0. (1-1106)

Величина (индекс для общности опущен) определяется выражением

LVDx; (1-111)

она имеет размерность длины и носит название средней диффузшн-ной длины или средней длины диффузии. Физический смысл величины L будет ясен из дальнейшего.

Остановимся сначала на стационарном уравнении (1-1106). Как известно, его решение является суммой двух экспонент:

,Др(х) = Л1е--1-Л2Л, (1-112)

где коэффициенты Ai и А определяются из граничных условий (обычно при X = О к X - w). Если ю == оо и Ар (оо) = О, то = = О и = Ар (0). Тогда

Ар(х) = Ар(0)е-Ч (1-113)

т. е. избыточные концентрации спадают по экспоненте. Это один из характерных случаев в теории полупроводниковых приборов.

Из выражения (1-113) следует, что диффузионная длина есть то расстояние, на котором концентрация диффундирующих носителей (при их экспоненциальном распределении) уменьшается в е раз. На участке длиной (3-4) L концентрация уменьшается в 20-50 раз, т. е. становится пренебрежимо малой по сравнению с исходной.

Дифференцируя (1-113), получаем градиент концентрации:

На инжектирующей плоскости, т. е. в точке л; = О,

(0)=-. (1-1146)

Как видим, при экспоненциальном распределении носителей градиент их концентрации (в том числе начальный) пропорционален избыточной концентрации в каждой данной точке.

В процессе диффузии избыточные носители (в нашем случае - дырки) приобретагот определенную скорость, которую можно оценить из соотношения (см. сноску * на с. 42):

где д Ар - плотность заряда избыточных дырок.

Используя выражения (1-73а), (1-114а) и опуская для общности индекс р, получаем диффузионную скорость в виде

v,.=1- = . (1-115)