Это же выражение можно получить непосредственно из формулы (5-68). Поскольку при малых значениях сечение дырочного слоя и концентрация дырок в нем почти не зависят от х, величину обычно называют сопротшлением канала.

Из (5-68) и (5-696) очевидно, что остаточное напряжение на MJXn транзисторном ключе имеет чисто омическое происхождение:

VcoIcRo-

Это обстоятельство является важным преимуществом МДП транзисторов, так как в случае биполярных транзисторов даже при нулевом токе имеется вполне конечное остаточное напряжение [см. (15-10в)].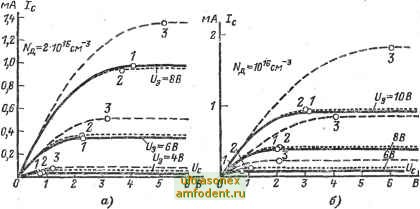

Рис. 5-32. Вольт-амперкые характеристики Л1ДП транзистора, построенные по (5-54) (сплошные линии), (5-58) (крупный пунктир) и (5-70) (Мелкий пунктир).

/-3 - точки насыщения соответствующих кривых; а - случай сравнительно высокоомной подложки; б - случай сравнительно низкоомной подложки.

Характеристики и параметры во 2-м приближении. Аппроксимация (5-58) и связанные с нею выражения вполне пригодны для приближенных расчетов и качественных оценок. Однако напряжение насыщения, а значит, и ток насыщения определяются при этом со значительной погрешностью, особенно в случае низкоомных подложек. Эта погрешность может достигать 50% (рис. 5-32). Еще большая погрешность получается тогда, когда потенциал подложки отличен от нуля, что часто имеет место в интегральных схемах. Поэтому иногда приходится использовать более точные аппроксимации, которые рассматриваются ниже.

Пусть потенциал подложки по-прежнему равен нулю, но желательно отразить влияние членов в степени входящих в выражение (5-54), сохранив при этом удобную форму выражения (5-58). Наиболее простой путь решения такой задачи состоит в следующем.

Вместо 1-го приближения (5-58) примем 2-е:

iU3~Uo)U,-il + n)Ul\, (5-70)

в котором поправочный коэффициент ц нужно выбрать так, чтобы напряжения насыщения f/с.н. определенные из (5-70) и (5-54), были достаточно близки друг к другу. Поскольку напряжение (Ус.н получается из условия dlJdU = О, продифференцируем правые части (5-70) и (5-54) и приравняем эти производные. Тогда коэффициент Г) после некоторых преобразований можно записать в виде

где тп - UJ2(fsm- Поскольку выражение (5-70) действительно лишь для ненасыщенного режима (т. е. при < f/с.н), не имеет смысла рассматривать сколь угодно большие значения т. Также не имеет смысла рассматривать значения m < 1, так как при этом действительно 1-е приближение (5-58) (см. с. 304). Разумным диапазоном можно считать m = 2 15. Тогда, как показывают расчеты, коэффициент Г) можно принять не зависящим от напряжения и равным:

Используя параметры, характерные для кремниевых МОП

транзисторов, получаем: т] = 0,8-10 1/д- Например, если d = = 10- см и Л/д = 10 см-з (т. е. р . 0,8 Ом-см), то tj ж 0,8. Из рис. 5-32 видно, что аппроксимация (5-70) обеспечивает высокую

ТОЧРЮСТЬ.

Дифференцируя (5-70) по U. и полагая dIJdUc ~ О, находим напряжение насыщения:

fc. = . . (5-72)

Оно оказывается меньше, чем при расчете по (5-59). Подставляя (5-72) в (5-70), получаем уточненную характеристику МДП транзистора в режиме насыщения [ср. с (5-60) :

/e = Yb(t/3-W (5-73)

где . .

- эквивалентная удельная крутизна, несколько меньшая реальной (5-55).

Естественно, что крутизна S и добротность Д, определяемые Величиной Ь, будут во 2-м приближении тоже в 1 -j- tj раз меньше,

чем в 1-м:

S = T(f/3-f/o); (5-75)

Для ключевого режима, характерного малыми напряжениями Uc, остаются в силе выражения (5-68) и (5-69), полученные из 1-го приближения.

Для тех (сравнительно редких) случаев, когда желательно описать вольт-амперные характеристики в целом, отразив и насыщенный и ненасыщенный режим в 1104] предложена эмпирическая аппроксимация:

/, = 6 {,Ug-U,r- ( /с.и) [1-0.5 th {UjUc. )]

Эта. формула, в которой t/c.H= Сз-в предельных режимах Uc < fc.H и {/с > fcH лает результаты, близкие соответственно к (5-58) и (5-60); в то же время она отражает конечный наклон кривых в режиме насыщения [и даже факт роста сопротивления Ri с увеличением напряжения Uc, см. (5-66)J

Влияние потенциала подложки. Пусть подложка имеет относительно истока положительный потенциал U . Тогда падение напряжения на обедненном слое при координате х будет уже не Ux, как считалось в формуле (5-49), г Ux + U- Соответственно и в формуле (5-51) нужно заменить Ux на Ux + U . Эта поправка, как легко убедиться, приводит к росту составляющей порогового напряжения f/os: вместо (5-57) получаем выражение

чв = ]/ф. +/п + фт, (5-77)

а вместо (5-56) - выражение

и, = Uop-\- КфЙп ф.,т. (5-78)

Характеристика (5-54) остается в силе с соответствующими поправками:

/с == b {(t/з - и ф,ш) f/c - - f/i - 4 g [(ф,+f/ -f Ucf -

-{!.m-\-Unm]. (5-79)

Что касается аппроксимаций, то оба приближения (5-58) и (5-70) остаются в силе, если для порогового напряжения использовать значение (5-78). Кроме того, в выражении (5-71) следует заменить фда на :

а/Со (5.80)

3rq -ft/ -