достаточно малой В целом условие (20-23) является более слабым, чем (20-106), так как последний член (20-23) можно всегда сделать меньше, чем rg/r*.

Приравнивая (20-22а) и (20-226), получаем для определения длительности импульса трансцендентное уравнение, которое после преобразований можно записать в форме

(20-24)

где = т,/т; &г = ч/х; i> = TJx.

В общем случае решение уравнения (20-24) кропотливо. Однако это решение можно облегчить, если учесть, что на практике задача ставится следующим образом: известны параметры

транзистора (т, р, г), коэффициент трансформации 6 и нагрузка Ri требуется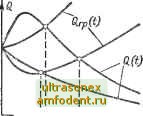

Рис. 20-7. Возможные влды функций заряда в базе Q и граничного заряда Qrp.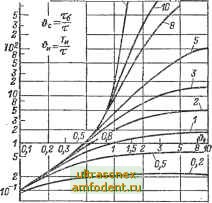

Рис. 20-8. Семейство характеристик функции (дс; Ov,), используемой при расчете длительности импульса.

найти значения величин и (т. е. по существу значения С и L), обеспечивающие заданное время Т. Для решения этой задачи целесообразно преобразовать уравнение (20-24). Пренебрежем величиной 1/Р в правой части и введем обозначение

(20-25)

Кроме того, введем обозначения для двух величин в левой Части уравнения (20-24):

е и.

(20-2ба) (20-266)

с учетом введенных обозначений уравнение (20-24) приводится к следующей форме, удобной для расчетов:

g(*c; * ) = Лх() ) + Л2 (20-27)

По исходным значениям о , Р определяются коэффициенты Ах и Лд. После этого, задаваясгэ одним из параметров [Ьс или &/.) и исполгэзуя кривые на рис. 20-8, находим второй параметр. Например, если а = 5; Р = 100 к = 3, то Лх 1 и An ~ 0,6. Полагая = 0,5, получаем ~ 2,2 и &с ~ 0,8, а полагая = 2. получаем 7 к 0,1.

Заметим, что заданное значение & можно реализовать только при достаточно больших значенияхО и Так, если в предыдуш,ем примере положить == 3 и = 0,2, то 5 0,3 и необходимое значение будет отрицательным, а ccjiH положить & = 0,01, то I = 61 и это значение при == 3 нельзя получить ни при каких значениях О. Ограничения на параметры и уже отмечались выше в связи с неравенством (20-23), которое соответствует реализации импульса с нулевой длительностью (# = 0).

В последующем анализе будут использоваться упрощенные выражения для функции ; они получаются при достаточно больших или достаточно малых значениях ©с и А именно, если &с > 4 и ©и > 3, то выражение (20-25) приводится к виду

5я= Ле-*и/ с; (20-28а)

а если <}с < 0.2 и > 2, то

l&c. (20-286)

Условие (20-23) показывает, что в принципе блокинг-генератор сохраняет работоспособность при наличии только одной реактивности: С или L. Случай С = оо, когда исчезает понятие независимой паузы, используется в преобразователях постоянного напряжения (см. § 22-2, рис. 22-5).

Часто желательно, чтобы сопротивление нагрузки (если оно меняется) не оказывало влияния на длительность импульса. Для этого необходимо выполнить условие Ах < AIl 1см. уравнение (20-27)1, откуда легко получается неравенство

L < TaR т/?И 1 + К). (20-29)

Здесь под Ra понимается минимальное сопротивление нагрузки. Случай Кбшыхолостого хода, характеризуемый неравенством (20-29), распространен на практике. Поэтому рассмотрим его подроб-

Еще два варианта неравенств > 4 и ©и < 0,5 или < 0,2 и < 0. приводят к одному и тому же приближению: &и. Можно показать, что в этих случаях условие (20-23) вьшолняется очень слабо, т. е. указанные варианты практически неприемлемы.

нее. Из условия S = Alii получаем необходимое значение индуктивности:

L = (20-ЗОа,

В случае длинных импульсов и большой постоянной времени в цепи базы подставляем (20-28а); тогда после преобразований

Например, если rg = С)м; т = 5 мкс: = 50 мкс; Р = 50; С = 1,5 мкФ; Пб = 0,2, то L 50 мкГ.

В случае малой постоянной времени в цепи базы и достаточно длинных импульсов в формулу (20-ЗОа) подставляем (20-28в) и после преобразования получаем:

(20-ЗОв)

(при выводе положено т/рдат). Например, если т = 0,1 мкс; Г = 2 мкс; Пб = 0.2; С = 0,01 мкФ, то L 100 мкГ.

Формулы (20-30) приводят к важному выводу, который можно получить также из общего выражения (20-24): время импульса находится в прямой зависимости от индуктивности L и емкости С. Это понятно и из физических соображений, поскольку бесконечно большие значения L vi С означают стационарное насыщение транзистора, т. е бесконечно длинный импульс. В случае конечной (достаточ!ГО низкоомной) нагрузки, когда неравенство (20-29) не имеет места, длительность импульса уменьшается, т. е. зависимость Т от R тоже прямая. Действительно, учитывая в уравнении (20-27) член Ai, мы должны заменить значение g в формуле (20-ЗОа) значением - А-. Следовательно, уменьшение Ra сопровождается как бы уменьшением g; поэтому при неизменном значении L должно уменьшиться значение Т.

До сих пор считалось, что ток базы начинает спадать в самом начале вершины [см. (20-19)1- Однако при достаточно больших времязадающих емкостях (обычно при С > 0,1 мкФ) наблюдается существенное возрастание базового тока в течение некоторого времени и только после этого ток начинает уменьшаться (показано пунктиром на рис. 20-4). Такое явление [170] объясняется модуляцией сопротивления /-б накапливающимися в базе носителями (см. рис. 15-7). В самом деле, в момент / = О заряд сосредоточен в активной области базы, так как насыщение транзистора происходит в течение очень короткого переднего фронта. Затем дырки за время порядка т распространяются в пассивную область базы и сопротивление/ б уменьшается. Если напряжение б-Ек-t/c. Действующее в цепи базы, уменьшается с постоянной времени большей, чем т, то базовый ток будет возрастать до тех пор, пока лб достигнет установившегося значения. Получающийся выброс базового тока может в 2-3 раза превышать начальное значение /б (0).

Если рассчитывать емкость С, исходя из немодулироваиного начального значения rQ, то получающееся возрастание базового тока затянет первый этап формирования вершины. Зато последующий этап, когда ток I5 уменьшается, будет