токах она доходит до десятков и сотен микровольт на градус. Таким образом, в диапазоне ±60° С можно добиться (подбором транзистора и режима) температурного дрейфа около 100 мкВ.

Не меньшую роль для усилителей постоянного тока играет временнйя стабильность напряжения UВ этом отношении приходится ориентироваться только на эксперимент, который показывает [151], что временной дрейф имеет индивидуальный характер у разных типов и экземпляров транзисторов. Как правило, р течение первых 1-2 ч работы дрейф может составить несколько милливольт, а в дальнейшем он лежит в пределах 50-200 мкВ.

Погрешность сдвига можно существенно (в 5-10 раз) уменьшить и, следовательно, повысить чувствительность прерывателя, если использовать балансные схемы [148, 121]. Пример такой схемы 1Г10казан на рис. 15-9. Принцип компенсации состоит в том, что в отсутствие входного сигнала = 0) потенциалы Up и Uq одинаковы и иык - 0. как и требуется для устранения погрешности сдвига. Равенство Up = Uq возможно при условиях Igi -

= -/э2 и Ugi = -Us2-

Поскольку один из транзисторов закрыт, а другой открыт, равенство модулей и одновременно различие в знаках величин /э и Ug могут быть

обеспечены только тогда, когда рабочая точка первого транзистора лежит на линии запирания в IV квадранте, а рабочая точка второго - на линии отпирания во II квадранте (см. рис. 15-8, б).

Суммарные сопротивления + и Rr + R должны быть одинаковыми, а их значение выбирается таким, чтобы линия нагрузки Rj. + Rg, проведенная из начала координат, обеспечила равенство \ Ua\ = Ui,\ или I / I = 1 1 на рис. 15-8. Такой выбор осуществляется графически или по приближенной формуле:

Rg+RrUc/Ic;

последняя получена из графического построения при условиях UclRKlc, UdRo>Ic.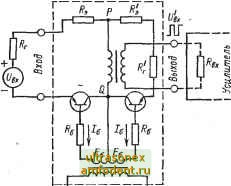

Модулирующее напряжение -О О-

Рнс. 15-9.

Однотактный компенсированный прерыватель.

Для схемы ОЭ (см. рис. 15-8, а) рабочими квадрантами характеристик Удут соответственно II н IV.

Переходные процессы в прерывателях подчиняются общим законам динамики транзисторных ключей (см. § 15-5) и потому отдельно не рассматриваются. Некоторые особенности переходных процессов, а также дополнительные сведения о прерывателях можно найти в монографии [151].

15-4. МЕТОД ЗАРЯДА

Прежде чем анализировать переходные процессы в транзисторном ключе, рассмотрим метод, с помощью которого такой анализ проводится гораздо проще, чем при использовании уравнений непрерывности. В основе этого метода, назьшаемого методом заряда [153, 154], лежит условие нейтральности базы (см. § 1-7). Согласно этому условию в любой точке базы положительный и отрицательный заряды одинаковы и изменяются с одинаковой скоростью. В базе типа п положительный заряд обусловлен донорами и дырками, а отрицательный - только электронами. Следовательно, исходя из условия нейтральности, можно записать:

Q + Qp = Qn-Дифференцируя обе части по времени, получаем: dQ, dQ, dQ,

Здесь каждое слагаемое имеет размерность тока, и задача состоит в том, чтобы установить связь этих слагаемых с теми токами, которые задаются при расчете или могут быть вычислены.

Изменение заряда доноров Qд связано с изменением толщины базы или, что то же самое, ширины переходов. Иначе говоря, первое слагаемое равно сумме токов, перезаряжающих барьерные емкости:

rfQ dU, dU

- Са -г; г Ск

di dt dt

Изменение электронного заряда Q обусловлено тремя причинами: базовым током, рекомбинацией в базе и электронными составляющими токов 4 и / . Последние всегда отрицательны, так как в процессе инжекции электроны у х о д я т из базы. Рекомбинацион-ный ток тоже отрицателен, так как рекомбинация приводит к уменьшению числа электронов. Поскольку речь идет о рекомбинации неравновесных электронов, из формулы (1-516), интегрируя по объему, легко получить для этого тока значение -AQn/t, где AQ - неравновесный заряд электронов. Тогда в целом

dt €

Как видно, встационарном режиме (dQJdt= 0) ток базы состоит из двух компонентов, один из которых обусловлен рекомбинацией, а второй - электронными потоками через переходы. В нестационарном режиме добавляется третий компонент {dQJdt), обусловленный накоплением электронов в базе.

Здесь / - сумма электронных токов через переходы, причем токи могут быть обусловлены как инжекцией электронов в смежный слой, так и рекомбинацией в области переходов. Подставляя полученные значения производных в (15-23) и учитывая, что AQ = AQp, получаем следующее дифференциальное уравнение для неравновесного дырочного заряда:

dUg dUg dQ AQ

C- + C + T + -Y = -- (15-24a)

Первый член в левой части, а также ток / в правой части не всегда существенны. Поэтому практически пользуются уравнением

+ 1 + (15-246)

и еще более упрощенным его вариантом

+ 4- =/б, (15-24В)

в которых опущены индекс р и знак Д.

Удобство выражений (15-24) заключается в том, что они в отличие от уравнений непрерывности представляют собой обыкновенные дифференциапьные уравнения, решать которые проще: нужно знать только начальные условия.

Практическое использование метода заряда подразумевает еще наличие простой связи между тем внутренним параметром - зарядом, который получается из приведенных уравнений, и таким внешним параметром, как коллекторный ток, который обычно представляет главный интерес при анализе.

В активном режиме транзистора связь между неравновесным зарядом Q и током содержится в выражениях (4-62) и (4-136). Запишем их в следующем общем виде:

где т] = О для бездрейфовых транзисторов.

Переходя от времени пролета д/1 + т] к времени жизни т, можно записать (15-25а) в другой форме :

Qfh. (15-256)

Эта форма соответствует наиболее распространенной схеме ОЭ с усилительным параметром - коэффициентом р. Выражения (15-25) основаны на допущении о квазистационарном распре-Делении заряда в базе; во время коротких переходных процессов они дают большую погрешность. Поскольку любые возмущения

Связь мезвду временем диффузии (в общем случае - временем пролета) и временем жизни вытекает из соотношений (4-85) и (4-82).