.. Таблица 1-2

Основные физические константы, используемые в теории полупроводников

порциональный ему кбсзыимпульс или волновое число к - р,

где h - постоянная Планка (см. табл. 1-2).

Для получения функции W (р) нужно так или иначе смоделировать кристаллическую решетку, отразив наличие внутренних полей и взаимодействия элек-

Запрщенные-. \ I зоны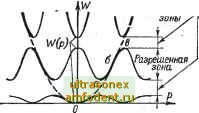

тронов и атомов [2-5, 71. В результате зависимость W (р) оказывается набором периодических функций, которые для простейшего одномерного случая показаны на рис. 1-10. Каждый периодический компонент соответствует разрешенной зоне, а расстояние между минимумами и максимумами смежных компонентов - запрещенной зоне. С ростом энергии ширина

разрешенных зон увеличивается, а ширина запрещенных зон уменьшается, что соответствует интерпретации зон на рис. 1-8, а.

Воспользуемся кривыми W (р) для анализа эффективной массы. Как известно, кинетическая энергия электрона может быть записана в виде

Рис. 1-10. Зависимость энергии электрона от импульса в одномерной кристаллической решетке.

2т

Если т = const (электрон в вакууме), то W - р, как показано на рис. 1-10 пунктирной параболой, В твердом теле функция W (р) описьшается кусочной кривой, показанной жирными линиями; эта кривая отличается от параболы и наличием разрывов, и формой непрерывных участков; следовательно, в твердом теле m const. Дифференцируя дважды функцию W {р), можно

определить эффективную массу электрона как

dW/dp ~{2л} dWIdk

и проследить за ее изменениями с помощью кривых W (р). Для всех зон результат будет один и тот же; ограничимся нижней зоной на рис. 1-10.

Между точками а и б имеем (PWIdp > О, т. е. т* > О, что соответствует обычномр электрону. Между точками б и б имеем dW/dp < О, т. е. т* <; О, что соответствует электрону с отрицательной массой. Наконец, в точке перегиба б имеем dW/dp = О, т.е. т* = =ь оо, и, значит (при конечном импульсе р), скорость V обращается в нуль; это соответствует ранее отмеченному резонансу между электронной волной и решеткой.

[111}

[100]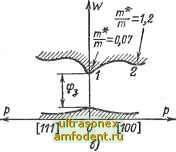

Рис. 1-11. Зонный рельеф кремния (а) и арсенида галлия (б) для двух кристаллографических направлений (ср. с верхней и средней кривыми на рис. 1-10 в пределах 1-го положительного полупериода ).

В начальной и конечной точках кривой (вблизи минимума и максимума) функция W (р) близка к квадратичной параболе, поэтому на этих участках значения кривизны dW/dp почти постоянны, а значит, почти постоянны и эффективные массы, однако они различаются не только по знаку, но и по величине.

В реальном трехмерном случае наглядная интерпретация функции W (р), где р - трехмерный вектор, невозможна, но основные представления, вытекающие, из одномерной модели, остаются в силе. Учитывая анизотропию кристалла, следует ожидать (и это подтверждается теорией), что в разных направлениях конфигурации зон, вообще говоря, будут различны. В частности, могут быть различными расстояния между разрешенными зонами. Поэтому под шириной аапрещентй зоны кристалла понимают расстояние между абсолютным минимумом зоны проводимости и абсолютным максимумом смежной (валентной) зоны. Как правило, эти два экстремума соответствуют разным импульсам р, т. е. расположены не друг под другом в пространстве импульсов. В этом случае переход электрона из одной зоны в другую должен сопровождаться не только изменением энергии, но и приращением импульса.

Учитывая периодичность функции W (р), ее достаточно анализировать в пределах одного периода , который в пространстве импульсов носит название зоны Бриллюдна [2, 7]. В частности, в пределах одной зоны Бриллюзна можно

рассмотреть полные рельефы дна зоны проводимости и потолка вдоль того или иного направления (рис. 1-11). Такие рельефы поз

валентной зоны

вдоль того или иного нипраьлении фис. i-iij. 1акис рсушсфЫ ПОЗВОЛЯЮТ оценить приращение импульса, необходимое для перехода из зоны в зону (см. выше), выбрать оптимальную плоскость шлифовки кристалла и т. п. Кроме того, из рис. 1-11, б следует, что достаточно энергичные электроны могут перейти из основного минимума / в побочный минимум 2, где они, как показывает теория, имеют меньшую подвижность. Это обстоятельство приводит к появлению отрицательного сопротивления (например, на кристалле арсенида галлия оказывается возможным строить генераторы СВЧ диапазона - генераторы Ганна [8]).

1-4. ЗОННАЯ СТРУКТУРА ПОЛУПРОВОДНИКОВ

При нулевой абсолютной температуре проводимость в собственном полупроводнике отсутствует, потому что зона проводимости пуста, а валентная зона заполнена. При любой температуре, отличной от нуля, в кристалле появляются фононы, энергетиче-

Зона проводимости-

-Валентная-

-30 на-

Зона проводимости

Уровни акцепторов

-Валентная}.

-зона-

Рис. 1-12. Зонные структуры полупроводников.

с - собственный полупроводник при Т фО К:, б - электронный полупроводник при Г = О К; в - дырочный полупроводник при г = о к.

ский спектр которых непрерывен. Фононы с энергией, превышающей ширину запрещенной зоны, переводят некоторые электроны из верхней части валентной зоны в зону проводимости (рис. 1-12, а). В результате в зоне проводимости появляются свободные электроны, а в валентной зоне - незаполненные уровни. Те и другие образуются одновременно и в равных количествах. Теперь электроны обеих зон могут двигаться в электрическом поле, обеспечивая проводимость кристалла.

Перевод электрона из валентной зоны в зону проводимости аналогичен возбуждению электрона в изолированном атоме, т. е. переводу его на один из верхних уровней. Такое возбужденное состояние, как известно, является временным: через некоторое время электрон в атоме возвращается на исходный уровень, а в твердом теле - в валентную зону. В корпускулярном аспекте это возвращение есть рекомбинация электрона и дырки. Среднее время возбужденного состояния электрона (т. е. пребывания его в зоне проводимости) в § 1-2 было названо временем жизни.