Численный коэффициент в формуле (15-39), разумеется, условен и зависит от того уровня заряда (относительно установившегося

значения /gixj, который принимается за критерий практического завершения экспоненциального процесса. Например, для уровня 0,9/б1Тн получится = = 2,3т (рис. 15-14). Если отпирающий импульс не бесконечная ступенька, а имеет конечную длительность сравнимую с постоянной времени т , то заряд в базе в момент /и будет меньше установившегося значения Ic. Величина Q {Q легко находится из выражения (15-34):

Рис. 15-13. Разделение полного заряда в базе на две составляющие, соответствующие собираемому и инжектируемому компонентам коллекторного тока.

и) = /б1Тн(1-е )

(15-41)

Накопление заряда в базе около переходов сопровождается увеличением положительных напряжений t/э и t/ji вплоть до их установивщихся значений, определяемых формулами (15-9). Рост указанных напряжений является внешним (хотя и не ярко выраженным) проявлением процесса накопления (рис. 15-14). Поскольку токи /э и /к в области насьщения не меняются, остаются неизменными и градиенты концентрации дырок на границах переходов. Таким образом, граничная кривая распределения (см. рис. 15-10), начиная с момента перемещается вверх параллельно самой себе. Скорость этого перемещения можно оценить, определяя производную uQIdt из формулы (15-34) и учитывая, что dQ ~ йр.

В дрейфовых транзисторах, характерных сравнительно толстым и высокоомным коллекторным слоем, накопление избыточных носителей происходит не только в базе, но и в коллекторе. Действительно, считая рб ~ Рк, приходим к вьшоду, что коэффициент инжекции коллектора в режиме насыщения далек от единицы [см. (2-35), где Рэ нужно заменить на pj. Значит, наряду с инжекцией дырок из коллектора в базу имеет место заметная инжекция электронов из базы в коллектор. В связи с большой величиной р время жизни электронов в коллекторе сравнительно велико, а следовательно, велика и диффузионная длина. В результате в коллекторе накапливается заряд избыточных электронов и соответствующий заряд компенсирующих дырок.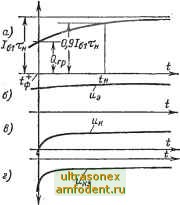

Рис. 15-14.

Накопление в базе.

носителей

а - заряд

базе, б и в - напряжения на переходах; г - потенциал коллектора.

в диффузионном приближении накопленный заряд можно оценить по формуле (2-84), заменяя р (0) на п (0) и w на ш. Однако на самом деле в слое коллектора имеется электрическое поле, обусловленное напряжением /ккк. причем дрейф носителей под действием этого поля оказывается более существенным, чем диффузия их. С учетом дрейфа оценка неравновесного заряда AQ k согласно [157] приводит к выражению

АС к<?5к/г(0)-??.

Qrp t

Основная доля заряда обычно накапливается не в активной, а в пассивной области коллектора, т. е. в области, расположенной вне проекции эмиттерного перехода на коллекторный (рис. 4-36). В целом заряд коллектора может существенно превышать заряд базы.

Накопление коллекторного заряда происходит в течение того времени, когда граничная концентрация р (w) повышается от нуля до установившегося значения (см. рис. 15-10), т. е. с постоянной времени х.

Рассасывание носителей. Пусть в некоторый момент времени входной ток ключа скачком уменьшается от положительного значения /gi до отрицательного значения /бг (рис. 15-15, а) *.

Отрицательный перепад тока означает отсос заряда, и потому последний, естественно, начинает уменьшаться. Однако, как и в заряженной емкости, заряд не может измениться скачком, не может мгновенно измениться и распределение заряда в базе. Следовательно, в течение некоторого времени граничные концентрации дырок у обоих переходов остаются выше равновесной концентрации и напряжения и сохраняют небольшую положительную величину. Очевидно, что ток коллектора при этом практически не меняется, а ток эмиттера уменьшается скачком в начальный момент на величину А/ = A/g, а затем остается неизменным. Все указанные процессы объединяют названием стадии рассасывания. Главное внешнее проявление этой стадии состоит в задержке начала фронта относительно момента поступления запирающего сигнала (рис. 15-15, в). Эта задержка характеризуется временем рассасывания tp - специфичным и важным параметром ключевого режима транзистора.

Рис. 15-15. Рассасывание носителей в базе.

а - входной ток; б - заряд в базе; в - ток нагрузки.

* Ток /б2 может быть и положительным, но должен иметь значение /б2 < < /к.н/р. достаточно малое для выхода транзистора из насыщения. Однако при положительном токе 12 транзистор не может запереться, т. е. вернуться к исходному состоянию. Поэтому случай /б2 < О (рнс. 15-15) более типичен.

Для анализа процесса рассасывания воспользуемся опять уравнением заряда, но в форме (15-28а), в которой учтен отличный от нуля начальный заряд. Подставив ток la и заменив т на Тн, получим изображение заряда

Q(s)

sQ(0)-b/62

которому соответствует оригинал

Q(0 = Q(0)e п + 1 тЛ1-е Ч (15-42)

Рассасывание закончится тогда, когда избыточный заряд в базе исчезнет и будет иметь место равенство Q = Qp. Подставив Qrp в левую часть (15-42), легко найти время рассасывания в следующем общем виде:

/pTjny-/;; . (15-43а)

Используя выражения (15-41) и (15-27) соответственно для Q (0) и и полагая в последнем т = т , выразим время рассасывания через управляющие токи:

/ =x ln/?Al=l JVziZl2. (15.436)

Здесь t - длительность отпирающего сигнала /gi. Если эта длительность значительно превышает величину Тц, получается более простая формула:

#=т 1п-/1=, (15-43B)

Эта формула широко применяется на практике, причем нередко забывают, что ее справедливость ограничена достаточно длинным отпирающим импульсом.

Вводя в формулу (15-43в) величину запирающего импульса А/б = hi - 62 и используя определение степени насыщения (15-8), можно привести время к виду

. = -xJn(l

* Мы не вводим специального индекса для постоянной времени рассасьша- ния, хотя она значительно (на 20-25%) меньше, чем постоянная времени насыщения. Различие объясняется тем, что накопление начинается при малом заряде в базе, а рассасьшание - при большом, когда поверхностная рекомбинация иг-, рает значительную роль. Таким образом, постоянную времени Тц следует измерять раздельно при отпирании и запирании ключа.