Из структуры выражения (1-S3) следует важный вывод о двух вариантах механизма релаксации. К именно, предположим, что полупроводник д ы р о ч н ы й и в нем создано начальное возмущение Ар (0) при An (0) = 0. Тогда, поскольку электронов в окружающем объеме очень мало и они не могут нейтрализовать (скомпенсировать) возмущение Ар (0), релак- .

сация будет состоять в йр(0)=-(0)

Ap(SrJ

Apfr)

[~1 Ap(Sr)

An(rJ Ап(3%) б)

j(Sts) An(t)

An(Jt)

уменьшении концентрации Ар благодаря уходу избыточных дырок из начального объема. Процесс рассасывания будет описываться выражением

Др = Др(0) ее

и закончится через время, равное примерно ЗТе (рис. 1-28. а).

Предположим теперь, что в том же дырочном полупроводнике начальное возмущение представляет собой избыточную концентрацию электронов Art (0) при Ар (0) = 0. Тогда релаксация будет состоять в нейтрализации (компенсации) заряда электронов An (0) дырками, приходящими под действием поля из внешнего объема, где их очень много. Процесс нейтрализации описывается выражением

Ap = An(0){l-g- 4

т. е. характеризуется увеличением концентрации Ар от О до An (0) и заканчивается, как и в первом случае, через Зт. После этого с гораздо меньшей скоростью, определяемой временем жизни т, будет происходить рекомбинация электронов и дырок, скопившихся в области возмущения (рис. 1-28, б).

Таким образом, если начальное возмущение вызвано основными носителями, то процессы рассасывания объемного заряда и избыточной концентрации происходят с одной и той же малой постоянной времени Tg. Если же начальное возмущение вызвано

An(0)=j(0)

Рис. 1-28. Схематическое изображение процессов диэлектрической релаксации в примесном (дырочном) полупроводнике.

а - исходное возмущение вызвано осиоеиеыми носителями; б - исходное возмущение вызвано неосновными носителями.

Заметим, что нейтрализация в принципе не может быть полной, иначе нельзя было бы объяснить наличие градиента концентрации дырок ме.чаду рассматриваемым объемом и основной частью кристалла. В действительности остается небольшой нескомпенсированньш заряд элеюронов, поле которого и поддерживает градиент концентрации дырок. Именно неполной ко.мпеысацией заряда объясняется термин квазинейтральность. Электрическое поле, обусловленное неполной компенсацией заряда, будем называть остаточным.

неосновными носителями, то нейтрализация объемного заряда заканчивается столь же быстро, с малой постоянной времени Те, а рассасывание обеих избыточных концентраций - значительно медленнее (уже в условиях квазинейтральности) с постоянной времени т. Второй вариант процесса является одной из основ транзисторной техники.

Начальное возмущение может выражаться не только в увеличении, но и в уменьшении соответствующих концентраций. При этом в уравнении (1-83) меняются только знаки при избыточных концентрациях; характер процессов остается прежним.

Введение ( впрь1скввани€ ) неосновных носителей в примесный полупроводник называют инжещией, а их отсасывание с образованием отрицательного возмущения - экстракцией.

Эффект поля. Пусть между металлической пластинкой и полупроводником задано напряжение U (рис. 1-29, а). Такая система представляет собой своеобразный конденсатор, у которого одна из обкладок полупроводниковая. На этой обкладке будет наведен такой же суммарный заряд, как и на металлической, но в отличие от металла заряд в полупроводнике не будет сосредоточен на поверхности, а распределится на некоторое расстояние в глубь кристалла. Распределение заряда, электрического поля и пот1Циала можно оценить, используя уравнение Пуассона (1-80). Специфика задачи в данном случае состоит в том, что плотность заряда Я, не является заданной. Она согласно (1-81) определяется концентрациями подвижных носителей, а эти концентрации в свою очередь зависят от распределения потенциала ф£. Поэтому прежде всего остановимся на зависимостях п (ф) и р (фв).

Заметим, что в рассматриваемой системе полупроводник, несмотря на наличие внутреннего индуцированного поля, находится Б состоянии больцмановского равновесия, так как нет результирующего тока. Значит, уровень Ферми во всех частях полупроводника постоянный: (fp = const. Для определения этого уровня воспользуемся формулами (1-18). Обозначим концентрации носителей и электростатический потенциал в правой, невозмущенной части полупроводника (рис. 1-29, а) через щ, Ро и фо и положим для простоты ф£о = 0. Тогда из (1-18) находим

Ф. = фИп = -Фг1п.

Подставляя найденное значение ф в (1-17), получаем искомые зависимости п (фг) и р (ф):

n = noe-V 7-; ]

потенциал ф отсчитывается от середины запрещенной зоны в нейтральной части полупроводника. Зависимости (1-85) позволяют решать уравнение Пуассона.

Рассмотрим сначала собственный полупроводник. В этом случае в (1-81а) следует положить N = Nt = О и подставить концентрации (1-85), считая По = Ро = Левую часть (1-80)

Металл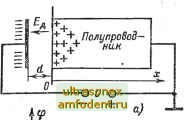

У7Т77777777777777

4>v

4>

4>e 9eo=0

Ve

Инверсионный, слой.

Рис. 1-29. Эффект поля в полупроводниках.

Схема эксперимента (а); распределение потенциала, поля, заряда и концентрации носителей в собственном полупроводнике при отрнцательной (б) и положительной (в) полярностях напряжения на металлическомэлектроде; распределение потенциала в примесном (электронном) полупроводнике при положительной (гУ п отрицательной (5, е) полярностях напряжения на металлическом электроде (модуль напряжения U для случая е значительно больше,

чем для случая б).

запишем как (Pffg/dx, поделим обе части на и введем безразмерную переменную Ф = Фв/фт-. Тогда уравнение Пуассона приводится

к вшу

d4D 1

(1-86)