Для типичных значений ре = (2 10) Ом-см и и L = 100 мкм ток /д (при площади S = 0,01 см) составляет 1-6 мА. В этих пределах (при данной площади) действительно выражение (2-33).

Сравнивая (2-65) и (2-70в), нетрудно заметить, что токи /в и /в близки друг к другу, т. е. вырождение экспоненциальной характеристики в омическую совпадает с переходом от низкого к высокому уровню инжекции.

Особенности, связанные с высоким уровнем инжекции (когда 61), следующие.

1. Концентрация дырок вблизи перехода становится сравнимой с концентрацией электронов. В связи с этим на участке, протяженность которого примерно равна диффузионной длине, заметную роль начинает играть дрейфовая составляющая дырочного тока.

2. Увеличение избыточных концентраций Др и Дп вблизи перехода приводит к существенному увеличению удельной проводимости базы в этой области (назовем этот участок модулированным). Модуляция сопротивления базы сказывается на коэффициенте инжекции (2-35) и на омическом падении напряжения Uq (2-63).

Дрейфовая составляющая тока инжектированных носителей. Полагая коэффициент инжекции близким к единице, будем по-прежнему считать, что полный электронный ток на эмиттерной границе базы значительно меньше дырочного; в первом приближении можно положить / = 0. Тогда напряженность поля в базе будет выражаться формулой (1-91). Подставляя это значение Е в (1-72а) и учитывая соотношение (1-74), получаем дрейфовую составляющую дырочного тока:

Если использовать условия квазинейтральности (1-50), то производную dn/dx можно заменить на dp/dx, а концентрацию п записать как По -f Др; кроме того, положим р = Др, поскольку Др > Ро- Тогда

Как видим, дрейфовую составляющую удалось привести к такой же форме, как и диффузионную (1-73а). Складывая обе составляющие, получаем полный дырочный ток вблизи перехода:

Здесь произведение в квадратных скобках можно считать э к-Бивалентным коэффициентом диффузии, значение которого зависит от уровня инжекции. При высоком уровне инжекции (Др (0) По) эквивалентный коэффициент диффузии близок к 2Dp. Следовательно, при высоком уровне инжекции дрейфовая составляющая дырочного тока почти равна диффузионной составляющей, а значит, полный дырочный ток можно рассчиты-

вать по диффузионной формуле.(2-33), удваивая получаемые значения:

...

I2I,fiT. (2-73)

Как видим, учет дрейфовой составляющей не приводит к качественным изменениям вольт-амперной характеристики диода.

Коэффициент инжекции. Как уже отмечалось, высокий уровень инжекции приводит к модуляции (уменьшению) удельного сопротивления базы.

Важным следствием модуляции базового сопротивления является уменьшение коэффициента инжекции, характеризующего долю дырочного тока на базовой границе перехода. Запишем граничную проводимость базы (при д; = 0) в виде

о, (0) = 1/Рб = Обо-f АОб (0) = Сб (1-f ,

где исходная проводимость базового слоя

а приращение проводимости (с учетом квазинейтральности) ЛОб (0) = Дп (0)-f Лр (0) 9И (1-f ) Лр (0).

Для простоты положим 1/Ь < 1; тогда Дсб (0)/Сбо 6 и, следовательно, согласно (2-35)

у1 (1+6). (2-74)

Такое приближение, столь же грубое, как и (2-35), действительно для значений у 0,95-ь0,9. Например, если pj pgo = 0,(Ю1, то формула (2-74) действительна для 6 50-н 1СЮ, т. е. для весьма высоких уровней инжекции.

Модуляция сопротивления базы. Повышенная концентрация носителей, свойственная высокому уровню инжекции, влияет не только на коэффициент инжекции (см. предыдущий раздел), но и на полное сопротивление базы г. Тем самым согласно (2-64) форма вольт-амперной характеристики зависит от уровня инжекции более сложно и более существенно, чем если бы эта зависимость определялась только увеличением эквивалентного коэффициента диффузии 1см. (2-72)].

Для того чтобы найти функцию (6), запишем сначала сопротивление элементарного слоя базы толщиной dx, расположенного вблизи перехода:

л - <ijc ~(Обо+Аоб)5

где (с учетом квазинейтральности, т. е. условия Дп ~ Др) ДОб = qiip Ар (X) + дцп An (х) q (l + Др [х).

Подставляя в выражение для Acg распределение (2-30) и интегрируя йг(, в пределах от л; = О до х =-w, можно привести сопротивление базы к следующему виду :

/-6(6)=-

/бо

(, ., A,+y2)(l ,+ /l+fe2)

(2-75)

(2-76)

а - сопротивление базы при низком уровне инжекции (2-62).

Графики функции (6) приведены на рис. 2-34 в относительном масштабе. Конечно, в общем виде зависимость (2-75) слишком сложна

для расчетов. Поэтому рассмотрим два частных случая, в которых эта зависимость существенно упрощается.

Пусть k < 1 (практически достаточно, если k < 0,5). Этот случай соответствует не очень высоким уровням инжекции или достаточно толстой базе. Тогда в формуле (2-75) можно положить = О, а также пренебречь величиной k везде, кроме первого члена знаменателя. Этот первый член {ke) с учетом (2-76) будет примерно равен 26 (по-0,Бе-/, если w/L 1). В результате после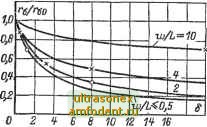

18 20

Рис. 2-34. Зависимость базового сопротивления от уровня инжекции и толщины базы.

скольку sh (w/L)

логарифмирования дроби получаем :

Гб(6)я Гбо 1 -ln(l-fS)

(2-77а)

На рис. 2-34 зависимость (2-77а) действительна для начальных участков кривых вплоть до точек, отмеченных знаком х.

Пусть теперь k 1 (практически достаточно, если k > 2). Этот случай соответствует высоким уровням инжекции или достаточно тонкой базе. Тогда в формуле (2-75) можно положить

* При интегрировании используется подстановка t/=e с соответствующей заменой пределов интегрирования.

2 Это выражение в несколько иной форме, а главное, без указания границ применимости приведено в (38].