Режим обеднения соответствует обратной полярности напряжения, при которой основные носители отталкивают с я от поверхности. В этом случае вместо тонкого канала с повышенной проводимостью образуется сравнительно толстый слой с пониженной проводимостью, в котором объемный заряд обусловлен ионами ( обнаженными атомами) примеси, от которых удалились основные носители (рис. 1-29, д). Протяженность этого слоя определяется не дебаевской длиной, а другим характеристическим параметром [ср. с (2-96)]:

(для дырочного полупроводника следует заменить N, на /VJ.

Хотя структура выражений (1-90а) и (1-906) одинакова (тем более, что По Лд), но есть и существенная разница, состоящая в том, что дебаевская длина 1о зависит т о л ь к о от свойств полупроводника, тогда как толщина объемного заряда Iq зависит еще и от приложенного напряжения, которое влияет на значение s-

С ростом обратного напряжения объемный заряд примесных ионов растет, а заряд основных носителей продолжает уменьшаться, но одновременно растет заряд неосновных носителей, притягиваемых к поверхности. Когда нарастающий заряд неосновных носителей превысит заряд оставшихся основных, изменится тип проводимости приповерхностного слоя. Этот случай характеризуют термином инверсия типа проводимости, а какал, образованный неосновными носителями, называют инверсионным слоем (рис. 1-29, е). Протяженность инверсионного слоя обычно составляет всего 0,001-0,002 мкм.

У металлов с их огромными концентрациями свободных носителей (обычно 10 см 8 и больше) характеристические длины и должны были бы составлять доли ангстрема. В действительности, если учитывать квантовые эффекты, проявляющиеся при таких расстояниях, заряд сосредоточивается на значительно большей глубине, равной нескольким ангстремам, т. е. нескольким межатомным расстояниям.

Неоднородные полупроводники. В конце § 1-7 отмечалось, что в неоднородных полупроводниках должны иметь место внутренние электрические поля (см. рис. 1-17, а). Определим зависимость внутреннего поля от степени неоднородности на примере электронного полупроводника, у которого концентрация доноров выражается функцией /Vj (х). Концентрация электронов в общем случае будет выражаться несколько иной функцией, однако для простоты примем п (х) = Л/д (х).

В основу анализа положим больцмановское равновесие, т. е. постоянство уровня Ферми: q>F = const. Дифференцируя по х обе части выражения (1-18а) и учитывая, что dqi/dx = Е, получаем напряженность внутреннего поля в следующем виде:

£=. ф. (1-91)

Соответственно с помощью (1-80) находим плотность объемного заряда:

, [fdn/dxY dn/dxl ооч

= eor[[-j-j--Г~\-.. )

Из выражений (Ь91) и (1-92) видно, что внутреннее поле и объемный заряд тем больи1е, чем резче меняется концентрация основных носителей и чем меньше эта концентрация в каждой данной точке.

Для того чтобы получить поле с заданной напряженностью и заданной конфигурации, необходимо обеспечить определенное распределение концентрации примесей N (х). В общем виде это еще не решенная технологическая задача. Практически приходится, наоборот, исходить из технологически реализуемых функций N (х) и анализировать соответствующие им поля.

Рассмотрим случай

Л/д(х) = Л/д(0)е- (1-93)

который реализуется при диффузионной технологии (см. § 4-13). В этом случае, считая п (х) = (х), из (1-91) и (1-92) получаем:

Е = (рт/Ь; (1-94)

к = 0. (1-95)

Как видим, при экспоненциальном распределении примеси электрическое поле имеет постоянную напряженность, а объемный заряд соответственно отсутствует Поле будет тем сильнее, чем меньше длина Ьд, характеризующая глубину проникновения примеси Б кристалл. Для типичных значений £д = 1 -т- 2 мкм получается £ 100 200 В/см.

Постоянное поле обусловлено, как и в обычном плоском конденсаторе, зарядами, сосредоточенными в тонких приповерхностных слоях при дс <=s О и X (рис. 1-30, а). Эти заряды образовались в результате небольшого сдвига электронов вдоль оси х под действием градиента концентрации dn/dx. Вблизи л = О остался нескомпенсированный (или не полностью скомпенсированный) положительный заряд обнаженных доноров, а вблизи х = w получился отрицательный заряд накопившихся избыточных электронов. Толщины заряженных слоев определяются соответствующими характеристическими длинами*. Эти длины различны при х О к х w из-за различия концентраций п (0) и п (w), см. (1-93). На протяжении этих длин напряженность поля, постоянная в основной части кристалла, падает до нуля в точках д: = О и х = ш. Соответственно уровни ф, ф и ф, которые меняются линейно в основной части кристалла, в слоях объемного заряда претерпевают изгибы.

Структура заряженных слоев представляет первостепенный интерес при анализе полупроводников со ступенчатой неоднородностью. Пусть в точке х = О концентрация доноров скачком меняется от Nдо Л/да (рис. 1-30, б) и пусть про-

* Параметры 1 и (1-90) характеризуют не только экранирование полупроводника от внешнего поля, но и экранирование внешнего пространства от внутреннего поля в полупроводнике (см. рис. 1-30, а, где £== О слева от точки О и справа от точки ш).

тяженности обоих однородных слоев слева и справа от этой точки очень велики (много больше соответствующих характеристических длин). Тогда в удаленных от x = О областях сохранится равновесное состояние, свойственное каждому из слоев, т. е. концентрации электронов будут соответственно и /iqj. Однако вблизи точки x = О, где имеется большой (в принципе бесконечно большой) градиент

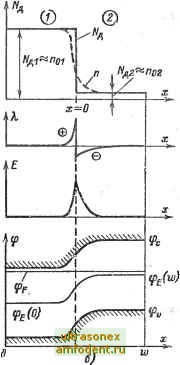Рис. 1-30. Распределение примеси, заряда, поля и потенциала в неоднородных полупроводниках.

а - плавная (экспоненциальная) неоднородность; б - ступенчатая неоднородность.

концентрации электронов, состояние не может остаться неизменным: часть электронов перейдет из слоя ] в слой 2. Следовательно, слева от точки х~ О останется некоторый нескомпенсированный заряд доноров, а справа появится заряд избыточных электронов. Образуется двойной электрический слой толщиной, примерно равной сумме характеристических длин, в пределах которого действует электрическое поле и существует разность потенциалов (рис. 1-30, б). Сравнительно резкие изменения потенциала, обусловленные объемными зарядами, называют пстенциальными барьерами.

В неоднородных полупроводниках характеристические д.пины и /о не являются однозначными параметрами материала, поскольку концентрации п и Л/ .заБисят от координат. Если, например, вычислить дебаевскую длину из выражения (1-9ба), подставив значение (х), то она будет.определять истинную протяженностъ объемного