рина перехода, во-вторых, изменяются граничные концентрации носителей. Рассмотрим эти зависимости на примере несимметричного перехода с низкоомным р-слоем.

Подставляя значение Дф из (2-10) в (2-96), получаем:

, -в Л2еоЕ(Дфо-<7) , -/ Дфо-t/

(2-11)

где /о - равновесная ширина потенциального барьера.

Как видим, переход сужается при прямом напряжении (U > 0) и расширяется при обратном напряжении (U < 0). Однако в первом случае полученное выражение является чисто качественным,

так как погрешность, обусловленная идеализацией перехода (пренебрежением зарядами подвижных носителей), оказывается более существенной, чем в равновесном состоянии. В то же время при обратном напряжении, удовлетворяющем неравенству I [/ I Фг, выражение (2-11) оказывается весьма точным и широко используется на практике. Особенно часто имеет место соотношение I f7 1 Дфо, при котором

Рис. 2-8. Смещение перехода в прямом (а) и обратном (б) направлениях.

/fell /- (2-12)

Подставляя в формулы (2-4) высоту барьера (2-10) вместо равновесного значения Дфо и считая концентрации основных носителей о н Рро неизменными, получаем для граничных концентраций неосновных носителей выражения:

Рп = РрФ~ - = (Рров- ет-

Пр = Ппф

Учитывая, что в скобках стоят равновесные граничные концентрации, определяемые формулами (2-4), запишем полученные выражения в следующей форме:

Рп--

Рп( П

Пр = ПрфЪ.

(2-13а) (2-136)

Если напряжение V приложено в прямом направлении, то согласно (2-13) концентрации р и р на границах перехода возрастают РО сравнению с равновесными значениями р о и ро. Иначе говоря, в каждом из слоев появляются избыточные неосновные носители, т. е. имеет место ипжекция (рис. 2-9, а).

Если напряжение U приложено в обратном направлении, то граничные концентрации р и Пр уменьшаются по сравнению с равновесными значениями, т. е. имеет место экстракция (рис. 2-9, б).

р-слой. г. п-слой.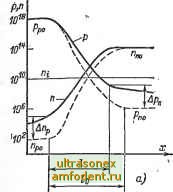

JQ18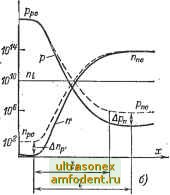

Рис. 29; Распределение носителей в кремниевом переходе при прямом (а) и обратном (б) напряжениях. Пунктиром показаны распределения в равновесном состоянии.

Значения избыточных концентраций на границах перехода найдем, вычитая из р и Пр соответственно равновесные концентрации Рпо и Про-

Арп = Рпо{е т-1); (2-14а)

Апр = Про{е- т-1). (2-146)

Сравним граничные избыточные концентрации в слоях р и п, разделив (2-14а) на (2-146) и заменив в правой части концентрации Рпо и Про на Рро и Ппо по формуле (1-16). Тогда

(2-15)

В несимметричных переходах концентрации рро и п о сильно различаются, поэтому концентрация инжектированных неосновных носителей будет гораздо больше в высокоомном слое, чем в низко-омном. Таким образом, в несимметричных переходах инжекция имеет односторонний характер: неосновные носители инжектируются в основном из низкоомного слоя в высокоомный.

Инжектирующий слой с относительно малым удельным сопротивлением называют эмиттером, а слой с относительно большим удельным сопротивлением, в который инжектируются неосновные Для него носители,- базой.

Формулы (2-13) и (2-14) подтверждают, что в режиме экстракции граничные концентрации неосновных носителей могут быть сколь

угодно малы, но всегда положительны, а избыточные концентрации отрицательны но по модулю всегда меньше равновесных значений (см. с. 85, п. 2). Обратные напряжения, при которых Рп < Рпо, Пр < Про и соответственно Ар -Рпо, АПр -Про. определяются условием

/>(3-4)фг. (2-16)

В дальнейшем запись \ U \ > (3-4) фт- будет пониматься именно в таком смысле. Заметим, что условие (2-16) применительно к прямым напряжениям означает р р о и Про, т. е. позволяет пренебречь единицей в выражениях (2-14).

В TeopiiH полупроводниковых диодов и транзисторов зависимости (2-13), (2-14) игракэт весьма важную роль, поэтому полезно исследовать границы их применимости. Для этого снедует напомнить, что указанные зависимости получены из (2-4) путем простой замены равновесной величины Афо на неравновесную величину Аф = Афо - и, а также в предположении неизменных концентраций основных носителей п о и Рро- Последнее предположение соот-вепствует условию низкого уровня инжекции в базе [см. (1-109)] . Что касается замены Афо на Аф, то в ее основе лежит понятие квази-равновесного (почти равновесного) состояния перехода при наличии внешнего напряжения. Действительно, поскольку выражения (2-4) получены из условия больцмановского равновесия (т. е. равенства диффузионных и дрейфовых составляющих токов в переходе), то использование этих же выражений для неравновесного состояния означает, что равновесие нарушено несущественно, т. е. результирующий (разностный) ток значительно меньше каждой из составляющих - диффузионной и дрейфовой: / /д ф /др.

Для того чтобы конкретизировать это условие квазиравновесия, нужно оценить одну из равновесных составляющих, например диффузионную. Строгая оценка затрудняется тем, что внутри перехода градиенты концентрации существенно меняются (рис. 2-3, б и 2-4). Поэтому ограничимся грубой оценкой применительно к дырочным токам, которые, как уже отмечалось, играют главную роль в несимметричном переходе с р+-эмиттером.

Средний градиент концентрации дырок в переходе примем равным [Рт - Рп (0)]/o. где р (0) = р о + Ар (0) Ар (0) (условие Др (0) > р о практически всегда выполняется). Этим градиентом согласно (1-73а) определяется составляющая /д ф в переходе. Что касается результирующего тока /, то он согласно (1-П6) определяется градиентом Др (0)/L , где Lp - диффузионная длина дырок в базе (Lp > у. Тогда из неравенства / < /диф легко получить условие квазиравновесия р+-п перехода:

На зонных диаграммах состояние квазиравновесия в переходе отражается почти горизонтальным расположением квазиуровней Ферми для дырок и

* Уровень инжекции в эмиттере, как следует из (2-15), всегда значительно ниже, чем в базе. Поэтому в большинстве реальных случаев можно считать Рр = - Р/.о= const для любых токов, тогда как концентрация /г с ростом тока может намного превысить равновесное значение ц, если уровень инжекции в базе много больше единицы.