Коллекторная цепь рассчитывается из соотношения

Ek = \U \ + I,R . (6-15)

где напряжение t/кб заранее известно, а одним из параметров или задаются. Соотношение (6-15) получается из общей формулы (6-5а) при [Уб = О-

Каскад с общим эмиттером. Рассмотрим сначала типичную схему (рис. 6-5), в которой Ев = = ER/iRi + Ri) п R = = Ri II Ri. Поскольку в уравнения (6-4в) и (6-8) [или (6-11)1 входят три неизвестные величины: Eq, Rq и R одной из них нужно задаться. Часто задаются сопротивлением Rq из условия, аналогичного (6-14):

R6 = RilR>R.., (6-16)

но иногда разумнее принять за основу сопротивление R, исходя из желательного значения напряжения = IsR.

В первом случае, выбрав R, находим R с помощью выражения (6-8), полагая ДУ А/к.доп:

(А/к.допб -At/зб)

к. 1тпп

л/ко-

-Re. (6-17а)

(l + P)J

Во втором случае, выбрав R, находим R:

/?б<-Р (А/к.допэ + Ауэб)--j. (6-176)

(1+Р)

если знаменатель (6-176) отрицательный, следует изменить знак . неравенства.

Задаваясь значением Д/к.доп. следует обеспечивать условие

А/к.доп2гД/ко+/э(12.- (6-18)

в противном случае формулы (6-17) недействительны. Иначе говоря, значение Дк.доп. не удовлетворяющую условию (6-18), нельзя реализовать ни при каки.х значениях и Rq.

Зная Rg и Re, нетрудно найти сопротивления делителя Ri и R. Для этого запишем потенциал базы в виде

Ue-Ee + hRe-E.f + IeRe и подставим Ue = -IgR - Ue- Тогда получим:

Сопротивление r2 легко выражается через и Rii

Из общей формулы (6-56) при = О получаем соотношение Ek\Uk,\ + IkRk + IsRs, (6-20)

исходя из которого можно определить э. д. с. или (если э. д. с. Ек задана) внести необходимые коррективы в значения R и R (последнее с точки зрения стабильности желательно изменять только в сторону увеличения).

Если каскад имеет структуру, показанную на рис. 6-6, то сопротивлением и напряжением £к задаваться не следует, так как в противном случае эта схема не будет иметь преимуществ перед предьщущей. Сопротивления Re и R выбираются с учетом условий (6-16) и (6-17). После этого нужно найти сопротивления Ri

и /?2-

Сопротивление Ri определяется из выражения (6-19а), если вместо э. д. с. J?k использовать напряжение == /э?э + IksI (w которого питается делитель в данной схеме):

Сопротивление R рассчитывается по формуле (6-196). Зная сумму Ry -j- R, выбирают /?к из условия

RviRi + Ri- (6-22)

Учитывая, что через сопротивление R протекают и ток коллектора, и ток делителя, напряжение £к определяют по формуле

В заключение заметим, что схемы на рис. 6-5 и 6-6 в действительности должны быть дополнены блокирующими конденсаторами. В противном случае усиление, даваемое каскадами, будет очень мало, так как обратные связи будут подавлять не только температурные приращения А/к, но и приращения, вызванные сигналом. Реальные схемы каскадов будут рассмотрены в следующей главе.

Каскад с общим коллектором. Как уже отмечалось, этот каскад (рис. 6-7) с точки зрения режима отличается от каскада ОЭ только отсутствием резистора R- Поэтому расчет сопротивлений проводится по формулам (6-17) и (6-19). Учитывая, что R = О, значение Rb согласно (6-20) можно выбрать значительно большим, чем в каскаде ОЭ. Это способствует повышению стабильности, а главное, позволяет увеличить сопротивление R и вместе с ним входное сопротивление каскада.

Глава седьмая

УСИЛИТЕЛИ С ЕМКОСТНОЙ СВЯЗЬЮ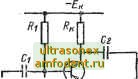

7-1. ВВЕДЕНИЕ

В транзисторных усилителях, как и в ламповых, наибольшее распространение имеют каскады с емкостной связью .

Типичный каскад такого типа (рис. 7-1) содержит переходные конденсаторы Ci и Cj и блокирующий конденсатор С д.

Конденсатор призван изолировать генератор (источник) сигнала от входа каскада по постоянному току и соединить их по переменной составляющей сигнала. Конденсатор выполняет аналогичную функцию по отношению к выходу каскада и нагрузке. Конденсатор шунтирует резистор по переменному току и тем самым ослабляет (практически ликвидирует) отрицательную обратную связь в каскаде на частоте сигнала.

Емкости ЭТИХ конденсаторов оказывают влияние на работу каскада в области низших частот и при передаче вершины импульсов. В области высших частот и при передаче фронтов импульсов первостепенное значение имеют временная (или частотная) зависимость коэффициента р и коллекторная емкость Ск. В отличие от ламповых схем паразитные емкости в транзисторных каскадах оказывают обычно второстепенное влияние и могут не учитываться.

Как и в других типах усилителей, при анализе транзисторных каскадов выделяют область средних частот, в которой можно считать схему состоящей только из активных элементов и не учитывать временных и частотных искажений. С этой области мы и начнем изучение каскада.

Однако предварительно сделаем два замечания. Входные сопротивления биполярных транзисторов, как правило, меньше, чем выходные. В связи с этим транзисторные каскады часто работают не как усилители напряжения, а как усилители тока [62]. Поэтому наряду с коэффициентом усиления

Рис. 7-1. Принципиальная схема каскада ОЭ с емкостной связью.

Ниже термин каскад (не совсем строго) используется применительно к одно каскадным усилителям - главным объектам анализа в данной части книги. Собственно каскады, т. е. элементарные промежуточные ячейки многокаскадного усилителя (см. рис. 7-16), являются частным случаем однокаскадных усилителей, когда источником сигнала служит выход предыдущего каскада, а нагрузкой - вход следующего каскада (см. § 7-4).

Что касается тезиса о распространенности емкостной связи, то он справедлив лишь для дискретных электронных схем, монтируемых из отдельных компонентов. В области интегральных микроэлектронных схем типичны гальванические, непосредственные связи между каскадами (см. гл. 13 и 14).