концентраций, происходящие вблизи эмиттера, распространяются до коллектора за время порядка Та, можно считать формулы (15-25) действительными тогда, когда длительность переходньа процессов превышает время распространения носителей вдоль базы.

Для решения уравнений (15-24) необходимо знать начальные значения заряда. Обычно эти начальные значения соответствуют

стационарным условиям, при которых все производные по времени равны нулю. Тогда получаем:

Q = /6T. (15-26)

т. е. в стационарном режиме неравновесный заряд дырок пропорционален базовому току. Это важное соотношение действительно не только в активной области, но и в области насыщения.

На границе активной области и области насыщения, когда еще действительны формулы (15-25), граничный заряд имеет величину: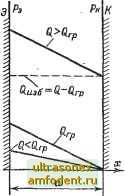

Рис. 15-10. Распределение дырок в базе при активном, граничном и насыщенном режимах.

Qrp- /к. в.

(15-27)

г Де /к.н - ток насыщения. Выражение (15-27), как и соотношения (15-25), действительно только при не очень коротких переходных процессах Величина граничного заряда широко используется при анализе насыщенных ключей в качестве критерия перехода их из активной области в область насыщения и обратно.

Выразив токи в формуле (15-8) через заряды (15-26) и (15-27), получим наглядную интерпретацию степени насыщения:

Q-Q,

Разность Q - Qrp~ Q s6 называют избыточным зарядом; следовательно, степень насыщения характеризует относительную величину избыточного заряда. На рис. 15-10 показано распределение концентрации дырок (и тем самым заряда) для разных режимов работы транзистора.

В тех случаях, когда переходные процессы анализируются операторным методом, следует записать уравнение заряда в операторной форме и найти изображение заряда. Воспользуемся сначала простейшим уравнением (15-24в). Подставляя общее соотношение dQIdt =i S [Q - Q (0)1, получаем:

Q(s)

/6(s)T-KsT)Q(0) 1 -i-sT

(l5-28a)

в частном случае, когда Q (0) = О, получаем:

Q(s) = -TSr- (5-286)

Отсюда, зная функцию tg (О и ее изображение /g (s), можно найти по таблицам оригинал Q (t) и затем с помощью (15-25) ток h (О-

Уравнение (15-24в) позволяет ввести понятие сильного управляющего сигнала, которое часто упрощает анализ ключевых схем. Пусть сначала ключ находился в стационарном режиме {dQfdt = 0), а затем ток базы скачком изменился на величину A/g. Поскольку заряд Q не может измениться мгновенно, получаем в первый момент: (dQ/dt) ~ Д/g; следовательно, заряд сначала меняется линейно:

AQWfl <=A/g<, (15-29а)

\UtJe

или в операторной форме

AQ(s). (15-296)

В активном режиме, когда действительно соотношение (15-256), аналогичные выражения получаются для коллекторного тока :

Д/Л0=А/б~; (15-ЗОа)

Мк (15-306)

Выражения (15-29) и (15-30) действительны при условии постоянства производной dQIdt. Согласно (15-24в) такое постоянство обеспечивается при выполнении неравенства

A/g> (15-31а)

или для активного режима [с учетом (15-256)1

А/б>Ц==. (15-316)

Неравенства (15-31) называют условиями сильного сигнала. Значения AQ и А/к в правых частях (15-31) легко оцениваются при конкретном анализе переходных процессов. Если неравенства (15-31) остаются в силе на протяжении всего фронта выходного импульса, то фронт оказывается почти линейным.

В тех случаях, когда нужно учитывать влияние коллекторной емкости, пользуются уравнением (15-246). Если нагрузка чисто активная (сопротивление r, следует подставить в (15-246) dU == = /?к/ и выразить d/к с помощью соотношения (15-256). Тогда легко привести (15-246) к следующему виду:

dQ , Q т .

ai ine ое

Чтобы получить формулы (15-30), достаточно заменить в соотношении (15-256) величины Q и на AQ и Д/н, после чего приравнять правые части выражений (15-29) и соотношения (15-256). Величина т/р принята равной t . Строго говоря, вместо t должно стоять время пролета (4-138) (для бездрейфовых транзисторов - это время диффузии tj.

где постоянная времени v заменяет т:

Гоет + СШк. (15-32а)

Полагая т = (1 + р) Та и деля обе части (15-32а) на 1 + Р, получим эквивалентную постоянную времени, которая заменяет Ха, если нужно учесть коллекторную емкость:

Тас Х + сл. (15-326)

Под емкостями Ск и Ск понимаются емкости, усредненные по диапазону напряжений. Согласно [147] такое усреднение приводит к результату Ск ~ 1,6 Ск {Е) в случае отпирания, когда напряжение меняется от до 0. и Ск ~ 2,1 Ск (Е) в случае запирания, когда напряжение меняется от О до Е. В сущности постоянные времени Хде и т ое те же, что и в усилительной технике [см. (7-36) и (10-7)]. Разница состоит только в том, что емкости Ск и Ск усреднены, а коэффициенты токораспределения Vk и Yk при постоянных времени т и t положены равными единице (в ключевых схемах редко учитывают сопротивления rS и г.

Легко убедиться, что в изображениях (15-28) учет емкости Су. приводит к замене т на Хое только в знаменателях и при члене Q (0). Условия сильного сигнала (15-31) с учетом емкости не меняются, а в выражениях (15-30) следует заменить Ха на Таое-

15-5. ПЕРЕХОДНЫЕ ХАРАКТЕРИСТИКИ КЛЮЧА ОЭ

Процесс замыкания транзисторного ключа можно разделить на три стадии: задержка, формирование положительного фронта выходного тока и накопление избыточного заряда в базе. Процесс размыкания ключа можно разделить на две стадии: рассасывание избыточного заряда и формирование отрицательного фронта. Анализ переходного процесса в транзисторном ключе был впервые проведен в работе [155] на основе эквивалентной схемы (рис. 4-9) с использованием операторных выражений для коэффициента а. Однако проще рассмотреть каждую из пяти стадий переходного процесса, используя для анализа уравнения заряда (15-24).

Задержка фронта. Эта стадия переходного процесса обусловлена перезарядкой барьерных емкостей Сд и Ск под действием входного сигнала. В исходном состоянии, когда ключ заперт, на базе транзистора имеется положительное смещение f/eo, обусловленное положительным входным сигналом Е = Евг, (рис. 15-1). Когда сигнал Eq скачком принимает отрицательное значение -Ei, призванное отпереть ключ, через сопротивление Re и входную емкость Свх начинает протекать ток. Поскольку напряжение на входной емкости не может измениться скачком, транзистор остается запертым вплоть до полного ее разряда. Емкость С перезаряжается от напряжения Ueo до -Egi по закону

с (О = 6 (О = (£б 1 + и6 о) е - £б I.