Отсюда легко получаем:

(7-7а)

В идеальном усилителе тока {R = оо), работающем в режиме короткого замыкания (/? = 0), имеем:

Выражение (7-7а) можно записать в виде

К/== Ягк.8вх1ыхЬ

(7-76)

(7-7B)

Rk+R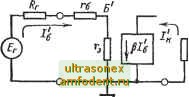

Rr + RB i?Bb,x + /?H

- коэффициенты входа и выхода каскада по току. Относительно индексов I и I будем придерживаться правил, аналогичных тем,

которые изложены выше в о , связи с формулами (7-4).

Внутренняя обратная связь. Из рис. 7-2 ясно, что в рассматриваемом каскаде имеет место обратная связь, поскольку часть коллекторного тока ответвляется во входную цепь. Для того чтобы исключить обратную связь, можно мысленно отсоединить генератор p/g от точки Б и заземлить его левый зажим (рис. 7-3); тогда выходной ток /к не будет влиять на ток источника сигнала (более строго вопросы внутренней обратной связи рассматриваются в § 8-3).

Коэффициент обратной связи в реальной схеме (рис. 7-2) определяется соотношением

Рис. 7-3. Случай отсутствующей внутренней обратной связи по току.

(7-8)

где - ток, задаваем ыйв узловую точку Б от н е з а в и -с и МО го генератора тока, заменяющего генератор p/g.

Элементарный расчет показывает, что в схеме на рис. 7-2 коэффициент обратной связи равен:

Аналогичная величина, действительная для полных токов и зависящая от внешних сопротивлений, встречалась при анализе температурной стабильности [см. (6-36), (6-46)].

Ниже нередко придется иметь дело с частным случаем выражения (7-9), когда Rf = О к токораспределение обусловлено только

сопротивлениями самого транзистора:

У.-Т- (7-10)

Заметим еще, что доля коллекторного тока, ответвляющаяся в цепь эмиттера, связана с коэффициентом у(, элементарным соотношением

Т. = 1-Тб. (7-11)

В предыдущем разделе параметры каскада ОЭ были получены непосредственно, но их же можно получить, учитывая наличие обратной связи, и представить в соответствующей форме. Для этого воспользуемся схемой на рис. 7-3 и запишем сначала параметры без обратной связи \

Bxrg-fr; (7-12)

Сравнивая выражения (7-12)-(7-14) с выражениями (7-2), (7-4а) и (7-7а), нетрудно убедиться, что они связаны вполне определенными соотношениями. А именно, входное сопротивление (7-2) получается, если умножить (7-12) на 1 -f Рубо

/?вх = (-б + /-а)(1+РТбо). (7-15)

а коэффициенты усиления (7-4а) и (7-7а) получаются путем деления выражений (7-13) и (7-14) на 1 + РТб

К Р 11 . (7-161

\ + ЫЯг + Гб + Гэ

Смысл этих формул следующий. Если обратной связи нет, то ток эквивалентного генератора p/g, а следовательно, и выходные ток и напряжение определяются входным током Iq (рис. 7-3). При наличии же обратной связи на ток /б накладывается ток обратной связи (р/б)7б:

/б = /б-(р/б)7б.

Отсюда результирующий ток

Коэффициент К получается из соотношения - (Рб (к н

где (R - /-g + г, а кдаффициент после представления источника

сигнала в виде генератора тока / , зашунтированного резистором R, - из соотношения 1= - (р/) \RJ {r\ + /? )], где \RJ {R, + г + г,)!-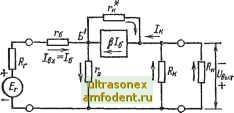

Как видим, ток базы уменьшается в 1 + у раз по сравнению со случаем отсутствия обратной связи. Соответственно уменьшаются выходные ток и напряжение, а значит, и коэффициент усиления.

Сравнивая выражения (7-16) и (7-17) с (7-13) и (7-14), легко заметить, что влияние обратной связи равносильно уменьшению коэффициента, передачи р е 1 + раз. Эквивалентный коэффициент передачи р/(1 + Pve). учитывающий внутреннюю обратную связь, является тем параметром, который-при анализе статического режима

каскада мы называли коэффициентом нестабильности [см. (6-7)].

Тот факт, что в выражении для входного сопротивления стоит коэффициент обратной связи Убо. а не 7б. объясняется тем, что параметр Rx определяется отношением bJh, а не EJI. Следовательно, для нахождения /?вх нужно полагать /?г = О (т. е. считать э. д. с. прилохенной непосредственно к входным зажимам: (Ух = г)-

Из выражений (7-15)-(7-17) следует, что обратная связь является отрицательной (см. § 8-3), так как она увеличивает входное сопротивление и уменьшает коэффициенты усиления (см. § 8-2).

Полный анализ. Главной причиной, ограничивающей коэффициент усиления Ка при высокоомной нагрузке, является сопротивление Гк (рис. 7-4), которое не было учтено при выводе формулы (7-4а). В ряде случаев оно оказывает влияние и на Другие параметры каскада.

Учесть наличие сопротивления Гк можно разными способами, в том числе заново анализируя схему методом контурных токов. Однако более наглядным и удобным представляется следующий путь. Введем коэффициент токораспределения в коллекторной цепи;

Рис. 7-4. Полная эквивалентная схема каскада в области средних частот.

(7-19а)

Этот коэффициент показывает, какая доля тока р/б поступает во в н е ш н ю ю цепь коллектора (остальная часть тока ответвляется в резистор tt) .

Во всех практических случаях R R г, поэтому (7-19а) упрощается:

(7-196)

Выражение {7-19а) имеет ту же структуру, что и (7-10), так как в обоих случаях ток распределяется по двум ветвям. В схеме на рис. 7-4 одна ветвь содержит резистор / *, а вторая- сложный резистор, эквивалентное сопротивление

которого в выражении (7-19а) помещено в. квадратные скобки.