работает так же, как в области средних частот. В дальнейшем, по мере заряда емкости Сг, входной ток не меняется, а ток и напряжение нагрузки уменьшаются. Для количественного анализа следует добавить к /?н операторное сопротивление l/(sC2).

В обоих случаях из выражения (7-4а) нетрудно получить изображение

Ku(s) = K,o-, (7-24)

в котором Кио - коэффициент усиления в области средних частот, а постоянная времени Тц имеет вид:

т 1 = Сх(/?г + /?вх) (7-25а)

для первой емкости и

т 2 = С2(/?к + /?н) (7-256)

для второй емкости.

Оригиналом изображения (7-24) является обычная экспоненциально спадающая функция (рис. 7-6):

/

Ku{t) = K oe е. (7-26)

Относительный спад вершины при достаточно коротком импульсе (4 тн) выражается известной формулой [62]:

(7.27)

(см, рис. 7-6).

В случае транзисторных каскадов получить малый спад б часто нелегко, поскольку постоянные времени ti и х можно увеличивать только путем увеличения емкостей. Последние должны быть весьма большими, так как сопротивления R, /?к и /? обычно не превышают нескольких килоом. Как правило, конденсаторы Ci и Cg - электролитические, с емкостями в десятки, а иногда и сотни микрофарад.

Частотные характеристики, обусловленные переходными конденсаторами, получаются из выражения (7-24) заменой оператора s иа /со:

= -(7-28)

(О

Нижние граничные частоты ©1 и 2 определяются как величины, обратные постоянным времени х и т 2 [см. (7-25)]. Частотная характеристика имеет такой же вид, как и в ламповом каскаде (рис. 7-7).

Влияние блокирующей емкости в цепи эмиттера. Положим С, = оо, Cg == оо и выясним роль емкости в переходном процессе.

в первый момент после поступления сигнала емкость Q закорачивает резистор Ra, т. е. начальные значения токов и напряжений такие же, как на средних частотах. По мере заряда конденсатора Cg уменьшается эмиттерный ток; вместе с ним уменьшаются ток базы и выходные величины. В пределе, когда конденсатор зарядится полностью и ток через него сделается равным нулю, сопротивление в эмиттерной цепи станет равным R + вместо начального значения г. Очевидно, что ток базы и выходные величины

Щых.

Рис. 7-6. Переходная характеристика в области больших времен (штриховая линия) и прямоугольный импульс с искаженной вершиной (жирная линия).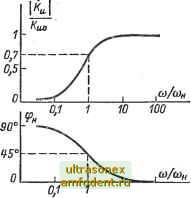

10 то

Рис. 7-7. Амплитудно- и фазо-частотная характеристики в области низших частот (сдвиг фазы на 180° в области средних частот не учитывается).

сильно уменьшаются за время переходного процесса, но их конечные значения будут все же отличны от нуля. В этом заключается принципиальная особенность влияния емкости по сравнению с влиянием емкостей и С. Постоянная времени переходного процесса равна произведению емкости на суммарное шунтирующее ее сопротивление. Последнее представляет собой параллельное соединение внешнего сопротивления R и внутреннего выходного сопротивления каскада со стороны эмиттера.

Для количественного анализа можно использовать формулу (7-4а), добавив к сопротивлению (входящ,ему в R) операторное сопротивление

1--8Тн.э

где Тн,э = Сэ/?э. После этого легко привести изображение коэффициента усиления к следующему виду:

К,! о

Ku{S)- (l + p)/?l/(R,-bJ?ex)

(7-29а)

I+sth. э

Отсюда видно, что в пределе, при = оо (т. е. при s = 0), коэффициент усиления будет гораздо меньше его начального значения. Так, при /?г = О и Гб < (1 + Р) Гэ получаем Ка (о°)/Ка (0) ~ ~ Гэ ?9, где Гд не превышает десятков ом, а Rg составляет 1 кОм и больше.

Практически можно считать Ка (°°) = О и в формуле (7-29а) пренебречь единицей по сравнению с членом 5Тн.э. Тогда изображение Ки (s) будет иметь ту же форму, что и (7-24):

Kais)Kuo . (7-296)

где постоянная времени равна:

т .. = Сд = Сд [гд j. (7-ЗОа)

Как видим, в таком приближении переходная характеристика является спадающей экспонентой (7-26), а ее постоянная времени не зависит от сопротивления Rg. Это значит, что последнее значительно больше, чем выходное сопротивление со стороны эмиттера, с которым оно включено параллельно. Если положить Rr + < (1 4- Р) Гд, что иногда имеет место, то постоянная времени запишется элементарно просто:

т .эСзГз. (7-306)

Сравнивая это выражение с выражениями (7-25), легко сделать вывод, что емкость Сд при прочих равных условиях должна быть значительно больше, чем переходные емкости, так как Гд < R и Гд < Ry.. Типичными значениями блокирующей емкости являются сотни микрофарад. Искажения вершины коротких импульсов рассчитываются по формуле (7-27).

Частотные характеристики, обусловленные емкостью Сд, получаются заменой оператора s на /со в (7-29). Если исходить из формулы (7-296), приходим к обычному выражению (7-28), в котором нижняя граничная частота сОн.э есть величина, обратная постоянным времени (7-30). Если исходить из полной формулы (7-29а), то при со = О получается конечное значение Ка, что соответствует структуре эквивалентной схемы.

Совместное влияние емкостей. Если одна из постоянных времени (Тн1, т 2 или Тн.э) много мсньше двух остальных, то именно она определяет переходную и частотную характеристики. В этом случае в формулы (7-26) и (7-28) следует подставлять наименьшее значение т или наибольшее значение со . Если же постоянные времени сравнимы, то анализ переходных и частотных характеристик усложняется. Однако в таких случаях главный интерес обычно представляют не сами характеристики, а результирующий спад вершины короткого импульса и результирующая граничная частота.