IcM. (15-1)1, поэтому эмиттерную цепь в таком режиме можно считать оборванной. Тогда эквивалентную схему триггера в исходном состоянии можно представить так, как показано на рис. 16-2. Воспользуемся этой схемой для вывода условий запирания и насыщения-транзисторов, а также для определения выходных величин и нагрузочной способности триггера.

Условие запирания транзистора. Для того чтобы транзистор Та был закрыт, нужно обеспечить положительный потенциал (Убг при наиболее неблагоприятных условиях. Обозначим запирающий потенциал через t/go и запишем его согласно рис. 16-2 в таком виде:

Ri+R

hoiRilRz)-

(16-1)

Полагая t/go > 0. приходим к

условию запирания

/?8<

(16-2)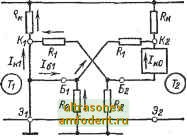

Эквивалентная

Рис. 16-2. Эквивалентная схема триггера в исходном состоянии (транзистор Tl насыщен, транзистор заперт).

которое с учетом допусков должно выполняться при минимальном значении Eq и максимальном значении /ко-

Обычно значение Eq бывает задано. Если же имеется возможность выбирать значение £g, необходимо учитывать, что с точки зрения длительности фронтов, как будет показано ниже, нежелательно глубокое запирание транзисторов. Поэтому при расчете быстродействующих триггеров следует ориентироваться на условие

(16-3)

В случае кремниевых транзисторов током Io можно пренебречь, но зато приходится учитывать напряжение Us.n на насьш1ен-ном транзисторе, которое нередко составляет 1 В и больше (см. § 15-2). Если на рис. 16-2 учесть потенциал Ui < О, то, как легко убедиться,

60 = Е, - и {Rll /?2) - и (16-4)

Фг<£б<(0,2--0,3)£,.

а условие запирания будет иметь вид:

/ко+кэ.н/?!

(16-5)

Как видим, для кремниевых транзисторов сопротивление /?а нельзя выбрать независимо от сопротивления R, которое оценивается на следующем этапе расчетов. Неравенство (16-3) остается в силе. .

в случае дрейфовых транзисторов значение Ua, ограничено пробоем эмиттерного перехода. Если пробой нежелателен, следует либо ограничить напряжение смещения:

£б</ роб(Ц-). (16-6)

либо ввести диодную фиксацию потенциала базы на уровне, меньшем t/npo6i либо включить последовательно с базой защитный диод (см. рис. 15-22).

Условие насыщения транзистора. Базовый ток насыщенного транзистора состоит из двух компонентов: тока обратной связи, вытекающего через сопротивление R, и тока, втекающего через сопротивление R. Ток обратной связи легко записать, учитывая, что он обусловлен двумя источниками - генератором э. д. с. и генератором тока /0- В результате получаем:

Коллекторный ток транзистора тоже состоит из двух компонентов: основного нагрузочного тока, вытекающего через сопротивление /?к, и паразитного тока обратной связи, втекающего через сопротивление Ri. Вторым компонентом, равным t/eo/Zi. вполне можно пренебречь, так как он на 1-2 порядка меньше первого. Таким образом,

/к1 = /к.н- §. (16-76)

Подставим выражения (16-7) в неравенство (15-7). Тогда последнее после некоторых преобразований можно записать в виде условия насыщения

Rx<R. в котором величину

1+Р 2

(16-8)

(16-9)

назовем фактором теплового тока. В случае кремниевых транзисторов можно считать д = 0. Условие (16-8) должно выполняться при минимальных значениях R, Р и максимальном значении О.

Из (16-8) следует, что сопротивление зависит в первую очередь от величины коллекторной нагрузки Последняя всегда известна в начале расчета: она выбирается исходя из желательной величины тока согласно (16-76).

Если сопротивление 2 оценивается из неравенства (16-2), то в неравенстве (16-8) величина R фигурирует как заданная и выбор сопротивления Rx не представляет затруднений. Если же

неравенство (16-2) недействительно (например, в случае кремниевых транзисторов), то сопротивления R2 и Ri следует определять, из системы двух неравенств (16-5) и (16-8). С этой целью обозначим правые части неравенств соответственно через /?2макс и 1макс и

построим зависимости /?2 акс (l) и /?1 акс (Rz) НЗ ОДНОМ И ТОМ Же

графике (рис. 16-3). Эти граничные кривые определяют область допустимых значений Ri и R2 [160].

В случае ненасыщенного триггера с нелинейной обратной связью выбор э. д. с. Еб и сопротивлений R, Ri производится так же, как указано выше. После этого обратная связь осуществляется по схеме, показанной на рис. 16-4 (здесь для большей ясности принято несколько иное начертание схемы, чем на рис. 16-1).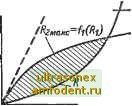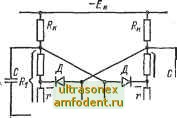

Рис. 16-3. Область допустимых значений Rx и R при их совместном выборе. Пунктиром показаны линии /?2накс для двух частных случаев.

Рис. 16-4. Симметричный триггер с нелинейной обратной связью.

Легко заметить, что отличие схемы на рис. 16-4 от схемы на рис. 16-1 заключается в следующем:

1. Сопротивление Ri разбито на две части, одна из которых (г) используется для получения э. д. с. фиксации (ср. с рис. 15-25).

2. Добавлены фиксирующие диоды Д. Такое решение соответствует ключу на рис. 15-25, и сопротивление г выбирается из условия (15-47), где нужно положить R(, = R.

Выходное напряжение и выходной ток. Выходным напряжением для схемы на рис. 16-1 является тот перепад потенциала, который получается при переходе транзистора из одного состояния в другое. Если в режиме насыщения можно принять О, то напряжение [/ых будет близко к потенциалу {/ запертого транзистора . Из рис. 16-2 легко найти 1/2 и, следовательно, {/ых в таком виде:

(16-10а)

-Rг+Rк

1 в ряде случаев приближение кэ.н= О недействительно; тогда выходное напряжение будет соответственно меньше приводимых ниже значений (16-10).