Складывая обе составляющие и II, получаем уравнение:

из которого легко определяются токи /д и al. Последний полностью протекает в цепи нагрузки и, следовательно, является искомым компонентом tj. Запишем ток if в следующем виде:

/ к \2 ~

(Rr+Гб+ГэГ

Поскольку э. д. с. S,s в схеме на рис. 4-29 включена последовательно с э. д. с. ёт.г, компонент i будет иметь такую же структуру/как (4-И 1а):

/ а \2 Zfi

= - ,г, . .-(4-1116)

Для определений-компонента , обусловленного источником тока i используем эквивалентную схему на рис. 4-30, б. Из нее методом суперпозиции (поочередно обрывая цепи al и tgg,) получаем:

Компонент ii, обусловленный источником тока Tg,g, определяется из эквивалентной схемы на рис. 4-30, в и равен сумме токов jg, + al, где ток а/ рассчитывается методом суперпозиции. В результате находим:

=(гаы-

Наконец, ток (дк полностью протекает в цепи нагрузки, не ответвляясь в цепь эмиттера, поэтому

= 1к- (4-П1Д)

Подставив полученные компоненты в (4-ИО) и используя формулы (4-108), нетрудно найти коэффициент шума схемы. Чтобы избежать громоздкого выражения, которое получается в общем случае, положим / э + Гб (т. е. = 1) и а = 1 (за исключением тех случаев, когда имеется двучлен 1 - а). Оба предположения вполне оправдываются на практике. Тогда после соответствующих преобразований и учета (1 -3) получим коэффициент шума в следующем виде:

. п.-1+ + [/кО + (1- )/а+1. (4-112)

где Л = Лз -Ь Лд.

Можно показать, что значение коэффициента шума почти не зависит от схемы включения транзистора, поэтому последующие выводы носят достаточно общий характер.

Анализ коэффициента шума. Из формулы (4-112) легко заметить, что, коэффициент шума имеет минимальное значение при определенном сопротивлении источника сигнала r. Дифференцируя

(4-112) по Rr и приравнивая производную нулю, легко найти значение оптимального сопротивления:

(4-113а)

Если соблюдается условие /о + A/2qf (1 - а) / то с учетом выражения (4-22) сопротивление R.om можно записать в сле- дующей форме:

(4-1136)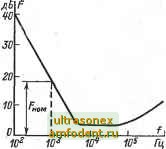

Рис. 4-31. Частотная характеристика коэффициента шума в логарифмическом масштабе.

Например, если Гб = 200 Ом; = 25 Ом и а = 0,98, то R. опт ~ ft; 700 Ом. Минимум функции (Rr) выражен неярко, поэтому увеличение и уменьшение сопротивления R в 2-3 раза по сравнению с Rr опт изменяют f всего лишь на 25-30%.

Выражение (4-112) показывает; что коэффициент шума зависит от диапазона частот: в области низких частот возрастает слагаемое A/2qf, а в области высоких частот - слагаемое /g (1 - а) (поскольку коэффициент а уменьшается с ростом частоты). Соответствующая частотная характеристика показана на рис. 4-31. При анализе шумов областью, средних частот является такой диапазон, в котором избыточные шумы уже несущественны, а заметный спад а еще ,не наступил. Этот диапазон обычно лежит в пределах от нескольких килогерц до сотен килогерц и выше. Оценим коэффициент шума в области средних частот, пренебрегая в формуле (4-112) членом A/2qf и подставляя = 1 мА; / = = 10 мкА; а = 0,98; rg = 200 Ом и найденное выше значение /?г = 700 Ом. Тогда получается характерное значение f щ я:; 2 (т. е. 3 дБ).

В области высоких частот в формуле (4-112) следует пренебречь членом AI2qf, а в качестве коэффициента а подставить модуль, соответствующий данной частоте. Например, если сохранить использованные ранее значения параметров и уменьшить а до 0,67 (это примерно соответствует частоте / ), то коэффициент шума будет иметь значение = 6,8 (т. е. 8,3 дБ). С физической точки зрения возрастание шумов в области высоких частот объясняется резким увеличением базового тока /б = (1 -а) и связанных с ним рекомбинационных флуктуации.

В области низких частот коэффициент шума быстро нарастает, н Практически в формуле (4-112) можно пренебречь всеми членами.

кроме A/2qf. Тогда получим для этой области: {

Как видим, параметр А* имеет сложную структуру и, в частности,.существенно зависит от значения сопротивления Rj.. Оптимальным значением в данном случае является R. = rg; оно меньше оптимального значения (4-113), найденного для широкого диапазона частот. Поскольку коэффициенты Ац А, входящие в состав параметра А*, рассчитать трудно, величину А* определяют экспериментально путем измерения коэффициента шума при определенном режиме транзистора, определенном значении R,. (обычно 0,5-1 кОм) и определенной частоте .(как правило, 1 кГц). Типичные значения коэффициента шума, измеренного таким путем лежат в пределах 10-2f0 дБ (f щ = Ю 100) для обычных транзисторов и 5-10 дБ (f ш = 4 -j- 10) для специальных талошумящих транзисторов [12, 661. Соответствующие значения А* составляют 10*-10* и 4-10* - 10* с . Отсюда легко оценить типичные значения коэффициента А в формуле (4-114). Полагая Rr = 500 Ом (т. е. R > Гб). получаем А = lOie \0г А; меньшее значение соответствует малошумящим транзисторам. .

Зависимость низкочастотных шумов от. режима определяется приближенными выражениями для коэффициентов и А, которые указаны в формулах (4-107). Однако эти зависимости носят качественный характер. Для количественных расчетов следует пользо-.ваться типовыми или индивидуальными кривыми, снятыми экспериментально.

Из формулы (4-112) видно, что при данной частоте коэффициент шума увеличивается с ростом рабочего тока [через член (1 - а), атакже через коэффициент Л] и температуры (через член /о)- Однако, для расчетов этих зависимостей также рекомендуется- использовать опытные данные.

Мощность и напряжение шума. .Приведем соотношения, связывающие ве-.личину коэффициента шума с мощностью и напряжением шумов на входе каскада [72]. Если в правой части формулы (4-109) разделить числитель и знаменатель иа коэффициент усиления мощности, то в числителе будет стоять полная мощность шумов, приведенная ко входу, а в знаменателе - мощность тепловых шумов в сопротивлении R. Последняя, как известно, равна:

PyA:kThf.

Поэтому приведенная (ко входу) мощность шумов выражается следующим образом:

P=AkTFISf\,Q-\G-Fhf. (4-115а).

Например, если = ЮО и Д/= 2 кГц, то Рш = З-10-i* Вт. Формула (4-115а) действительна только для белого шума или при условии < f; в противном случае нужно определять мощность путем интегрирования по диапазону часто-г. Так, в области низких частот, где спектр шумов имеет вид (4-114), получается выражение

Рш=4*ГЛ*]п&=3,6-10-20Л*18, (4-1156)

где h п h - граничные частоты. Пусть, например, Л* = 10 с *; /2=2 кГц; /1 = 50 Гц;, тогда Рщ = 6-ir Вт.