Переходим к построению желаемой ЛАЧХ. ЛАЧХ неизменяемой части имеет требуемый порядок астатизма и передаточный коэффициент, поэтому низкочастотная асимптота желаемой ЛАЧХ совпадает с низкочастотной асимптотой ЛАЧХ неизменяемой части системы.

Для заданного значения а = 30% по номограмме (см. рис. 5.24) определяем

Ртах=1.27 и ;р = 3,5я/(0ср-Вычисляем нижний предел частоты среза желаемой ЛАЧХ:

Мср1=3,5л/<р = 3,5л/0,5 = 22с-1. По (5.39) находим верхний предел частоты среза;

сйср2=Уй7§Г=У50/0,1 = 22,4 с-1.

Выбираем щ = 22 с- * и через эту точку проводим среднечастотнук> асимптоту желаемой ЛАЧХ с рекомендованным ранее наклоном

- 20 дВ/дек (рис. 5.28). Далее по кривым (см. рнс. 5.25) для Рщах = = 1,27 определяем, что необходим избыток фазы у = 40° при ординатах i-Ht (w), лежащих в пределах ±Lm = 14 дБ. Проводим прямую с ординатой + 14 дБ и из точки пересечения ее со среднечастотной асимптотой желаемой ЛАЧХ строим пробную сопрягающую асимптоту с наклоном - 40 дБ/дек.

Пусть высокочастотной асимптотой желаемой ЛАЧХ будет высокочастотная асимптота ЛАЧХ неизменяемой части системы. Сопряжение среднечастотной асимптоты желаемой ЛАЧХ с высокочастотной начинаем при частоте (о.

Теперь нужно проверить избыток фазы при контрольных частотах (Оа и соб. Воспользуемся номограммой для подсчета фазы по асимптотической ЛАЧХ, изображенной на рис. 5.26.

Подсчитываем фазу при частоте сйд:

Фа = -20 (2,25 -2,04) - 40 (2,04-0) - 20 (2,16-0) - - 40(2,2-2,16) - 60 (2,25 - 2,2) = - 133,6°. Следовательно, избыток фазы

Ya = 180-133,6 = 46,4°. Подсчитываем фазу при частоте we:

Фа = 20 (2.25-2,22)- (40 (2,22-2,16) - 20 (2.16-0,24)-

- 40 (0,24-Ц,12)-60 (2,25-1,12) = - 163.6

Избыток фазы при этой частоте

УО = 180-163,6=16,4°.

При частоте (Оа избыток фазы превышает требуемое значение на 6°. Допустимо, однако, лишь незначительное перемещение сопрягающей асимптоты вправо. Оно не расширит сколько-нибудь заметно диапазон пропускания нижних частот, поэтому останавливаемся ,иа выполненном сопряжении.

Избыток фазы прн частоте т значительно меньше допустимого. Для его увеличения высокочастотную асимптоту желаемой АЧХ нуж-

Рис. 5.29

HO сместить вправо. При этом усложнится корректирующее устрой-- ство.

Попробуем проверить качество системы при составленной желаемой ЛАЧХ и затем будем решать вопрос о целесообразности ее изменения.

По i- (w) составляем передаточную функцию разомкнутой скорректированной системы:

A:{s/C0a4-1)

S (s/w3-f I) (S/cu2+ I) (s/W4-f 1)

200(0,24s-f 1)

где шз = 0,46c-

s (2,17s+1) (0,01s+ 1) (0,00574s-f !)

(Oa = 4,2c-i; w2=100c- ; W4=174c-i.

Передаточная функция замкнутой системы

Wg (s) = lffWn+ W (s)J = (0,24 s + l)/(6,25 J0- +

-f 1,74-10- -f 0,01 Is-f 0,245 s-f 1).

Вещественная частотная характеристика, вычисленная по частотной передаточной функции Wg (/со), представлена на рис. 5.29. Пост- роенная по ней переходная характеристика показана на рис. 5.30.

Показатели качества а = 14% а tp = 0,4 с удовлетворяют требованиям. Перерегулирование даже значительно меньше допустимого, поэтому составленную желаемую ЛАЧХ можно ие изменять.

Несоответствие показателей качества с их расчетными значениями объясняется значительным отличием вида вещественной частотной характеристики скорректированной системы (рис. 5.29) от типовой, по которой составлены номограммы (см. рис. 5.24 и 5.25).

Вычитая из желаемой ЛАЧХ (со) ЛАЧХ Lq (со) неизменяемой части системы, получаем ЛАЧХ последовательного корректирующего устройства Ljf (со) (см. рис. 5.28). По этой ЛАЧХ составляем полиномы (s) и Qk (s) числителя и знаменателя передаточной функции корректирующего устройства:

/? (S) = (s/coa + 1) (s/coi + 1)=

= (0,24 s + 1) (0,05 s -f 1);

Q (s) = (s/w3 + 1) (s/щ + l) =

= (2.17s + 1) (0,0 0574s + 1).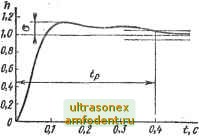

ex г у

>

Рис. 5.31

Желаемую передаточную функцию корректирующего устройства можно реализовать дифференцирующим и интегрирующим четырехполюсниками с разделительным усилителем (рис. 5.31).

Передаточная функция дифференцирующего четырехполюсника

VCm (s) = V a\s+l)/0\s+l),

где Ti = 0,05 RiCi; = 0,0574 = RTj(Ri + R.

Значение R должно быть выбрано при расчете усилителя. После этого могут быть определены необходимые значения /?i и Q и подсчитано значение йщ.

Передаточная функция интегрирующего четырехполюсника

где Гз = 0,24 = R Q; = 2,17 = (R + R) С.

Выбираем = 10 мкФ. Тогда R = 24 кОм и = 193 кОм.

Усилитель должен иметь коэффициент усиления Ку = k/k(,k i, где ко - передаточный коэффициент регулируемого объекта и исполнительного элемента.

Приближенные соотношения. Изложенный метод синтеза - это приближенный метод, поэтому рекомендуется [8] уточнять желаемую ЛАЧХ с помошд>ю номограмм.

Вместе с этим используют еще большие приближения, которые значительно упрощают построение желаемой ЛАЧХ и синтез корректирующего устройства.

На рис. 5.32 показана типовая ЛАЧХ разомкнутой астати-тической системы. Ей соответствует передаточная функция

s(ns+\){TaS+\) ТГз s(s + a)0(s + co3)

(5.47)

где > Tz>- Tg, tOi< t02< tOg; k - передаточный коэффициент разомкнутой системы (добротность по скорости), равный частоте ю, при которой продолжение низкочастотной асимптоты пересекает ось абсцисс (k = to).

Согласно [4], перерегулирование в системе не превзойдет 20-30%, если удовлетворяются неравенства

з/сог 10; 2 < (uJcHcp < 4.

(5.48)