л (ffl) = \W (/со)! =YU ( ) + V (ffl) -амплитудно-частотная характеристика; -ф (ю) = Arctg - фазочастотная характеристика разомкнутой системы без учета запаздывания;

фт:(а)) = ф (со) - сот (3,100)

- фазочастотная характеристика разомкнутой системы с запаздыванием.

Из (3.99) и (3.100) видно, что наличие запаздывающего звена не меняет модуля А (со) амплитудно-фазовой характеристики разомкнутой системы W (/м), а вносит лишь дополнительный отрицательный фазовый сдвиг ют, пропорциональный частоте, причем коэффициентом пропорциональности является время запаздывания т.

Зная амплитудно-фазовую характеристику W (/со) разомкнутой системы без запаздывания, легко построить амплитудно-фазовую характеристику Wx{jai) разомкнутой системы с запаздыванием. Для этого каждый модуль А (tOj-) вектора амплитудно-фазовой характеристики W (/ю) нужно повернуть на угол (OiX по часовой стрелке. С ростом частоты ш угол от будет быстро расти, а модуль А (ш) обычно уменьшается, поэтому амплитудно-фазовая характеристика Wxij) разомкнутой системы с запаздыванием -имеет вид спирали, закручивающейся вокруг начала координат (рис. 3.31). Закручивание амплитудно-фазовой характеристики из-за наличия дополнительного фазового сдвига сот, вообще говоря, ухудшает условие устойчивости, так как вся амплитудно-фазовая характеристика приближается к критической точке (-1, /0). Однако иногда при сложной форме амплитудно-фазовой характеристики W (/со) введение постоянного запаздывания может улучшить условия устойчивости.

Изменяя время запаздывания т в широких пределах, можно найти такое его значение, при котором замкнутая система будет находиться на границе устойчивости. В этом случае характеристика Wx (/со) будет проходить через точку (-1,/0).

Время запаздывания т р и

соответствующее ему значение частоты {о р, при кото-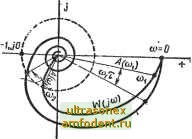

рых Wr (/со) проходит через точку (-1 ,/0), называют критическими.

Для критического случая справедливо следующее условие.

Wr ОЧр; = W (/ р) е- кркр = А (со р) е {*(кр)-кркр] =

-=--1. , (3.101)

Условие (3.101) можно записать раздельно для амплитуд и фаз вектора; WxUkp)-- -

Kp) = w?x(/co p) = i; (3.102)

(ю р) = Ф (со р) - р т р = -я (2t + 1), (3.103)

где / = О, 1, 2, 3, ... . в.

Из (3.102) можно найти сначала сог а затем из (3.103) найти Тир, т. е.

Окр кр Окр

Для систем автоматического управления с запаздьшанием основное значение имеет минимальное критическое время запаздывания (при i - 0), которое является в то же время и граничным

я-]-Arctg-i-

г - +(икр) . £/(соир) Ф(икр) (3.105)

кр о>кр о>кр

где ф (сокр) = я + Arc tg - запас устойчивости по фа-

Пример 3.10. Передаточная функция разомкнутой системы с запаздыванием

W.,(s)=/(e-=V(l+s7). , .

Определить критическое время запаздывания Ткр.

Частотная передаточная функция разомкнутой системы с запаздыванием

W. (/и) = Ке I + /соТ ).

Следовательно, условие (3.102) в данном случае

I (/ kp) \==m(l +/сокр т)] \=kyi-ЬсоДрГ= = 1. Из последнего выражения находим критическую частоту.

кр = Т/~/Г, К>1.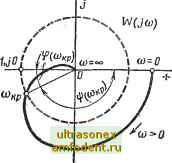

Рис. 3.32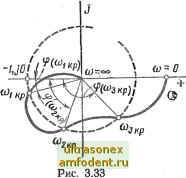

Фазовь!Й сдвиг на критической частоте

(сокр) = - Arctg кр 7 = - Arctg - -По (3.105) находим критическое время запаздывания:

я-Arctg УК - 1 я-Arctg У К - 1

Тир --~ Т---------

При сложном выражении для частотной передаточной функции W (/со) разомкнутой системы определение критического времени запаздывания просто выполнить графически. Условие А (сй р) = W (/св р)! = 1 определяется пересечением годографа W (/Ъ) с окружностью единичного радиуса с центром в начале координат (рис. 3.32). Точка пересечения определяет одновременно (о р и угол ф (сокр), который, будучи разделен на сокр, даст значение критического времени запаздывания.

Если имеется несколько точек пересечения годографа W (/(о) с окружностью единичного радиуса, например при WiKp, < )г р н (Одкр (рис. 3.33), то система будет иметь несколько критических граничных времен запаздывания:

11кр = фКкр)/Ю1ьр; Е2кр = ф(с02 р)/С02 р; Тз р=ф((Оз р)/(Оз ,

причем минимальное время запаздывания равно т р = = TiKp. Система будет устойчива при т < тр. а также при чгкр < т < Тзкр. Система будет* неустойчива при тр < т < < Сгкр, а также при т > Тдкр. Наблюдаемое в этом случае чередование участков устойчивости и неустойчивости системы