Задаваясь различными значениями частоты со, можно вычислить X (со) и Y (со), а затем построить границу D-разбиення, которая показана на рис. 3.28. Эта кривая также штрихуется слева по обходу при изменении частоты со от -оо до оо.

Кривая разбивает плоскость на четыре области: /, , / и IV. Претендентами на область устойчивости являются области lull. Проверим, является ли область / действительно областью устойчивости. При Ti = О характеристическое уравнение D (s) = (Т + 1) (7-38 + -f 1) -f /С = О является уравнением второго порядка с положительными коэффициентами; следовательно, оно имеет все левые корни.

Строго говоря, область / соответствует ТгфО к при этом характеристическое уравнение имеет третью степень. Прн уменьшении Тх одни из корней характеристического уравнения перемещается в плоскости корней влево н при Ti~Q становится отрицательным бесконечно большим. Исходя из теоремы о непрерывной зависимости корней от коэффициентов уравнения можно утверждать, что система будет оставаться устойчивой не только при 7 i = О, но и в некоторгой области малых значений Ti. Следовательно, область / является областью устойчивости D (0).

Далее, пересекая кривую D-разбнения по числу штриховок и нх направлению, размечаем области D (1) и D (2). Заметим, что в данном случае имеются две области устойчивости D (0).

Система будет устойчива прн О < Ti < 7 и при > 7 . Система будет неустойчива при TJ < < Т.

Пример 3.9. Рассмотрим ту же самую систему, что и в примере 3.8, но будем считать, что два параметра системы - коэффициент усиления разомкнутой системы К и постоянная времени - могут варьироваться одновременно.

Для определения влияния изменения этих параметров на устойчивость построим границу D-разбиения в плоскости двух параметров: Ti и К.

Перепишем характеристическое уравнение в виде D (s) = V [ГгГзб? + (Га -f Гз) -f s] + И + ТТ + {Т + -Ь Гз) S -Ь 1 = О,

где V = Г1; i = Я.

Подставляя в характеристическое уравнение s=j(a, получаем выражение для границы D-разбиения D (/w) = vN (/со) -4- iiM (/со) -Ь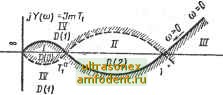

Рнс. 3.28

Приравняв нулю действительную и мнимую части, получим следующую систему двух уравнений:

:::)

- V (Га + Гз) ш 2 + г, Гз о> + 1 = о;

-V (Га Гз 0,3-и) +Ofi + (Ts + Т)а =

Решаем этн уравнения относительно v н ц:

V = (Га -ЬГз)/(Г2 Гз ft)2 1); из 1 f

+ (7., + Гз)2шМГаТзш-1). Главный определитель системы -(Г,-ЬГз)о)г 1 - (ГаГзЮ*-ю) О

= (ГаГзСо2-1)со.

Кривую D-разбиення можно построить, задаваясь значениями ча- тоты со от О до оо и вычисляя V н [X для фиксированных значений частоты. Однако на практике для облегчения построения сначала строят кривую D-разбиення качественно. Для этого качественно строят зависимость V и от со (или со), а затем, пользуясь имн и исключая со, строят качественную границу D-разбнеиия. Качественное построение v ~ = / (со) и [X = / (со), а также граница D-разбиения показаны на рис. 3.29.

Особые прямые находим, приравнивая нулю свободный член н коэффициент прн старшей степени s характеристического уравнения.

Особую прямую, соответствующую со = оо, находят нз выражении щ - T1T2TS = vTTs - О, откуда уравнение особой прямой v = 0.

Особую прямую, соответствующую со = О, находят из выражения л = 1 -f /С = 1 -f и = О, откуда уравнение особой прямой [х = - 1.

Кривую D-разбнення штрихуют двойной штриховкой при изменении частоты со от О до оо слева по обходу, если главный определитель Л > О, и справа по сйходу, если главный определитель Д < 0. Особые

прямые в данном случае штрихуют одинарной штриховкой, причем заштрихованные стороны прямых и кривой D-разбнення направлены

друг к другу.

Итак, главный определитель Д < О при О < со < vl/iTTs)

Д > О при со > yU{TTs).

Кривая D-разбиення и особые прямые делят плоскость (v, х) на шесть областей: /, , Ш, fV, V и VI. Претендентами на область устойчивости являются области I и IV. Рассмотрим точки, принадлежащие полупрямой х = /С = О при V = Ti > О, т. е. положительную часть оси абсцисс.

Прн /С = О и любом Ti > О характеристическое уравнение

D (S) = (1 + Tis) (1 + Т) (1 + Гз5) = 0:

следовательно, все три корня характеристического уравнения при этом будут левыми, т. е. Si = -l/Ti, Sg = -l/T и Sg = -l/Tg.

Таким образом, положительная часть оси абсцисс принадлежит области устойчивости D (0), а поэтому и вся область / являетси областью устойчивости.Переходя из этой области в другие через границу D-разбиения или особую прямую, размечаем остальные o6)iacTH D (1) и D (2). Заметим, что в данном случае имеются две области устойчивости D (0), однако нас будет интересовать только область устойчивости D (0), соответствующая физически осуществимым положительным значениям постоянной времени ti > О.

Построение границы D-разбиення в плоскости двух параметров дает полную картину влияния этих параметров на устойчивость системы. При малых значениях коэффициента усиления К система устойчива прн любых значениях Ti. При больших значениях К система устойчива лишь при достаточно малых либо достаточно больших значениях Ti, что совпадает с результатами, полученными в примере 3.8.

§ 3.9. Устойчивость систем с запаздыванием и систем с иррациональными звеньями

Системы автоматического управления могут содержать звенья, и которых зависимость между входной и (t) и выходной у (t) величинами имеет вид

у (t) и (t - х), (3.93)

где т - постоянная величина, называемая временем запаздывания. Такие звенья называют запаздывающими, так как они воспроизводят изменения входной величины без искажения, но с некоторым постоянным запаздыванием т.

передаточная функция запаздывающего звена (см. § 2.6)

Wsau(s)-e~\ (3.94)