Однако встречаются системы (с внутренними обратными связями), в которых потеря устойчивости может произойти не только при увеличении коэффициента усиления, но также и при его уменьшении. Этим случаям могут соответствовать так называемые клювообразные амплитудно-фазовые характеристики (рис. 3.20). В этих случаях запас устойчивости по амплитуде определяется величинами двух отрезков h оси абсцисс, заключенных между критической точкой (-1, /0) и амплитудно-фазовой характеристикой.

Чтобы система обладала требуемым запасом устойчивости при заданных величинах h и ф, около критической точки (-1, /0) вычерчивается некоторая запретная область в виде сектора, ограниченного величинами +/г и ±ф, в которую амплитудно-фазовая характеристика W (/со) не должна входить (рис. 3.20).

§ 3.7. Анализ устойчивости по логарифмическим частотным характеристикам

В инженерной практике широкое применение получил ана -ЛИЗ устойчивости систем автоматического управления, основанный на применении логарифмических частотных характеристик разомкнутой системы. Это обусловлено прежде всего тем, что построение логарифмических частотных характеристик разомкнутых систем, особенно -имптотических логарифмических частотных характеристик, значительно проще, чем построение годографа амплитудно-фазовых характеристик.

Покажем, каким требованиям должны удовлетворять логарифмическая амплитудно-частотная характеристика (ЛАХ) и логарифмическая фазочастотная характеристика (ЛФХ) разомкнутой системы, при которых обеспечивалась бы устойчивость системы в замкнутом состоянии.

Как было показано выше, устойчивость связана с числом переходов амплитудно-фазовой характеристики W (/со) отрезка (- оо , -I)-отрицательной вещественной полуоси. Когда амплитудно-фазовая характеристика W (/со) пересекает отрицательную вещественную полуось, ЛФХ пересекает одну из линий ± п {21 + 1), где i = О, 1,2, 3, ... (рис. 3.21). Переходы через эти линии не опасны с точки зрения устойчивости, если они совершаются справа от точки (- 1, / 0), т. е. если при этом модуль амплитудно-фазовой характеристики меньше единицы

Ц(/<й)<:1 и, следовательно, если ординаты ЛАХ отрицательны, т. е. Lm А (со) = 20 \g\W (/со)< 0. Поэтому область отрицательных ЛАХ при исследовании устойчивости интереса не представляет.

Положительному переходу (сверху вниз) через отрезок (-оо, -1) характеристики IF (/со) соответствует пересечение ЛФХ при Lm Л (со) > О прямых ± я (2г + 1) снизу вверх (точка 2 на рис. 3.21), а отрицательному переходу - сверху вниз (точка / на рис. 3.21).

Критерий устойчивости Найквиста применительно к логарифмическим частотным характеристикам может бьггь сформулирован следующим образом: для того чтобы система автоматического управления была устойчива, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов логарифмической фазочастотной характеристикой прямых ± (2i + 1), i = 0,1, 2,..., во всех областях, где логарифмическая амплитудно-частотная характеристика положительна LmA (со) > О, была равна 1/2 (t - число правых корней характеристического уравнения разомкнутой системы).

На рис. 3.21 приведены для примера амплитудно-фазовая характеристика разомкнутой системы W (/со) и соответствующие ей ЛАХ и ЛФХ. Из анализа этих ЛАХ и ЛФХ видно, что разность между числом положительных и отрицательных переходов ЛФХ прямых - п при Lm А (со) > О равна нулю. Таким образом, если разомкнутая система была устойчива (/ = 0), то и замкнутая система будет устойчива, при этом запасы устойчивости по амплитуде равны fiy и /Зг, а запас устойчивости по фазе равен ф.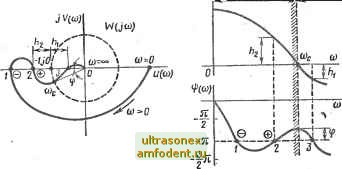

§ 3.8. Построение областей устойчивости в плоскости параметров системы

При исследовании устойчивости большое практическое значение имеет построение областей устойчивости в плоскости одного или каких-либо двух параметров, влияние которых на устойчивость исследуют, а также построение семейства областей устойчивости в плоскости двух параметров при различных фиксированных значениях третьего параметра.

Уравнение границ областей устойчивости можно находить, пользуясь любым критерием устойчивости! Однако чаще всего на практике применяют наиболее общий метод построения областей устойчивости, который был предложен Ю. И. Ней-марком. и назван им методом D-разбиения.

Понятие о D-разбиении, Рассмотрим характеристическое уравнение замкнутой системы л-го порядка, которое делением на коэффициент при переменном s с наивысшей степенью всегда может бьггь приведено к виду

Z)(s) = s + aiS -4-...+a =0, 0 = 1. (3.76)

Представим себе /г-мерное пространство, по координатным осям которого отложены коэффициенты уравнения (3.76). Это пространство называют пространством коэффициентов. Каждой точке пространства коэффициентов соответствуют конкретные числовые значения коэффициентов уравнения (3.76) и соответствующий им полином п-го порядка. Уравнение (3.76) имеет п корней, расположение которых на комплексной плоскости корней s зависит от числовых значений коэффициентов Gj.

Если изменять коэффициенты Ot уравнения (3.76), то его корни в силу их непрерывной зависимости от коэффициентов будут перемещаться в комплексной плоскости корней, описывая корневые годографы.

Чтобы представить сказанное выше геометрически, рассмотрим характеристическое уравнение третьего порядка (л =. 3)

D {s) = + Gis2+ а + as = 0. (3.77)

Если взять три взаимно перпендикулярные оси и откладывать по ним значения коэффициентов а, з. то получим трехмерное пространство коэффициентов, каждой точке которого соответствуют вполне определенный полином третьей сте-