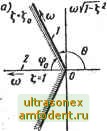Рис. 6.7

устойчивости. Например, при построении области изменения параметров р и ра исходя из расположения корней характери-ческого уравнения внутри угла 2ф в левой полуплоскости (рис. 6.7, а) используются формулы (6.65а) и (6.71). При построении областей изменения параметров с учетом заданной степени устойчивости (рис. 6.7, б) используются формулы, полученные для случая вещественных отрицательных корней характеристического уравнения, т. е. в формулы (6.65а) подставляются формулы (6.72а).

Пример 6.6. Рассмотрим характеристическое уравнение замкнутой системы

Со S*+Oi 9+oz +s 4 а* = О.

Коэффициенты характеристического уравнения зависят от двух параметров ft, и На линейно:

o,- = ajp,i-bPjH2 + Vi. = 0, 1,2,3,4.

и имеют вид Со = 0,04 уц; = 0,36 (л, + 0,04; - 2ц1 + 0,36; Оз= 2ц1 + 0,4Ц2+2; 04 = 2itj + 2.

Необходимо найти значения параметров (ij и для которых характеристическое уравнение имеет корни, расположенные слева от мнимой оси внутри угла ф = 60° (I = 0,5). Запишем коэффициенты характеристического уравнения следующим образом:

Ко = 0,04; Ро = 0; Vo = 0; = 0,36; Pi = 0; Vi = 0,04; =2; Р = 0; Ts = 0,36; 3 = 2; Рэ = 0,4; Va =2; 4 = 0; Р4 =2; Vi = 2.

Определим функции Q Qj, Qg для каждого значения со по рекуррентной формуле

Qft+,= -2a)Qft-ca Qft i(Qo=l; <?i=-2cag).

Для \ = 0,5 имеем Qo = 1 Qi = - = *)

Найдем коэффициенты Ау, By, Су, А, В, по формуле (р.71). Параметры Х и fi находятся из решения системы

Aifiy + ByHi+CyO;

откуда икгеем

AyBi

CyAi-CaAy

Л A : , А.Д-АаВу

при условии, что АуВ - АВу Ф 0.

Точки Ну и (ig при различных значениях <о образуют границу искомой области. Линии, соответствующие вещественным кориям.являют-ся особыми прямыми и определяются из .уравнения. (6.72),. Искомые области представлены на рис. 6.8.

Отметим, что каждому вещественному корню на плоскости параметров соответствует прямая. При практических расчетах это должно учитываться (как и в обычном методе С-разбне-ния) с помощью двух особых прямых. ;

: При использовании полиномов Чебышева проблема машинной штриховки по Неймарку остается нерешенной.В .случае построения областей устойчивости при различных степенях устойчивости могут быть использованы любые известные критерии, например критерий Рауса, а также прямые, корне-

вые мегодЫ. При построении области исходя из расположения корней-характеристического уравнения внутри угла, трапеции или в других областях слева от мнимой оси корневые методы являются единственно эффективными.

В заключение отметим, что модифицированный метод D-разбиения, основанный nai применении полиномов Чебышева, дает возможность вести исследование импульсных, гармо нически линеаризованных систем с одной или двумя нелиней-ностями. .. > ...

§ 6.11. Универсальные методы построения областей устойчивости и динамического качества

Если каким-либо образом найдена первая точка Границы области, можно обойти весь контур, двигаясь вдоЛь границы. Наиболее простой способ слежения состоит в йепользовании принципа взаимно-перпендикулярной ориентации.

Пусть построение границы искомой области происходит в двумерном пространстве, т. е. на плоскости. Алгоритй движения вдоль границы состоит в следующем. Направление изменения параметров на плоскости параметров р и Рз осуществляется в четырех возможных направлениях: вверх, вниз, влево, вправо, т. е. по сторонам квадрата. В вершинах квадратов проверяется выполнение условия G (pi, Рг) $

Если на данном шаге изменения параметров мы пересекаем границу и попадаем в искомую область, то G (pi, Ра) < / В этом случае следующий шаг выполняется с поворотом по часовой стрелке.

Если на очередном шаге изменения параметров мы пересекаем границу и выходим из искомой области, то G (pi, Ра) > > /. В этом случае следующий шаг изменения параметров выбирается таким образом, Чтобы движение происходило с поворотом против часовой стрелки. Легко видеть, что граница области находится в точке, где соблюдается условие G (pi, Рз) -I-

Получение более точного положения точки границы можно осуществить, применяя метод деления интервала, так, чтобы границы строились по точкам на расстоянии, равном половине стороны квадрата, или на расстояния, равном одной трети ее. Алгоритм движения вдоль границы искомой области иллюстрируется на рис. 6.9. При каждом пересечении границы