После определения предела а, к которому стремятся значения а,-, получаем

G (s) = (Kos/r + 1) (rs + ars+ 1).

где г = Cj - аод.

Пусть имеется полином четвертой степени

G(s)=aoS*+ais3+a2s2+fl!3S+l = ao (s+Ci s+cj s+Cg s+Cj),

где Ci = Oi/flc. = 02/oo, Сз ~ ag/flo. = l/ag. Вычисляем: 1 = с/4;з; Pj = di (Cy - Oj); Vi = 1 (ir - Pi); 2 = с4/(Сз - Yl); Pj = 2 (Ci - Юг); 2 (z - Рг) и т. д. Если процесс сходящийся, то

G (s) = (s/a + I) (as%4 + PsVci + ysfc + I).

где a, P и v - пределы, к которым стремятся соответственно а,-, Pj и Yi с увеличением i.

Полином третьей степени в полученном выражении в свою очередь нужно разложить на множители.

Если же процесс вычисления cj, pj и Yj расходящийся, то нужно вычислять

o.i=-Cg/c2-Pi = ai(ci-Xi)+C4/C2; 2= Сз/Ссг-Pi)-с4 (Ci--ai)/(C2-Pi); - Р2 = аа(с,-a2)+c4/(c2-Pi) и т.д.

В этом случае

О (s) - (aos/r2 + ns/r + I) (rs + arjs + I).

где a и P - пределы, к которым стремятся соответственно а,- и Р; Г1 Oi - асс; Гг = 2 - Рсо-

Порядок разложения иа множители полиномов пятого и шестого Порядков дан в [91.

После разложения полиномов (s) и Qo (s) передаточной функции Wo (s) на элементарные полиномы можно строить асимптотическую ЛАЧХ неизменяемой части системы. При этом нужно иметь в виду одно обстоятельство. В полиномах Ro (s) и Qo (s) могут оказаться сомножители с весьма малыми постоянными времени Tf. Их влияние на свойства системы (в частности, на ее устойчивость) незначительное, и при построении характеристики Ьо (со) такие сомножители можно не учитывать. Совершенно уверенно можно пренебречь двучленами и трехчленами, у которых Ti < JoOcuo - частота, при которой характеристика Lq (ю) пересекает ось абсцисс (частота среза этой характеристики). Пользуясь рекомендациями, сделанными в [1], можно более точно определить влияние малых постоянных времени и допустимость пренебрежения ими.

Примерный вид характеристики Ьо (ю) системы с астатизмом первого порядка показан на рис. 5.23.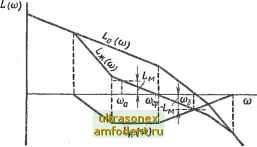

Рис. 5.23

Построение желаемой ЛАЧХ. Желаемой называют асимптотическую ЛАЧХ (со) разомкнутой системы, имеющейже-лаемые (требуемые) статические и динамические свойства. Желаемая ЛАЧХ (рис. 5.23) состоит из трех основных асимптот: низкочастотной, среднечастотной и высокочастотной. Кроме того, могут быть сопрягающие асимптоты, которые соединяют основные.

Строится желаемая ЛАЧХ на основании требований к системе. Ранее было выяснено, что низкочас:тотная асимптота ЛАЧХ разомкнутой системы определяет статические свойства. Если передаточная функция (5.37) разомкнутой- системы имеет передаточный коэффициент k и порядок астатизма v, удовлетворяющие требованиям, то низкочастотной асимптотой желаемой ЛАЧХ (to) является низкочастотная асимптота ЛАЧХ Lo (to) неизменяемой части системы. На рис. 5.23 показан именно такой случай.

Среднечас:тотнан ас:имптота ЛАЧХ разомкнутой системы и ее сопряжение с низкочастотной определяют динамические свойства системы - устойчивость и показатели качества переходной характеристики.

Построение среднечастотной асимптоты желаемой ЛАЧХ начинают с выбора частоты среза tOcp. Для этого используется номограмма (рис. 5.24), составленная В. В. Солодовниковым. Она определяет зависимос:ть перерегулирования а и времени регулирования р от максимума Рах вещественной частотной характеристики замкнутой сис:темы, причем время регулирования fp дано в виде функции частоты среза tOcp.

Номограмма используется следующим образом. По заданному значению перерегулирования а определяют значение

Рт&уц- Затем по

т. е.

определяют соотношение между н

(5.38)

р=СЯ/СОрр.

На рис. 5.24 показано, как по значению о = 30% определено Ртах = 1,27 и затем = 3,5я/соср.

Из (5.38) вычисляют частоту среза Wcpi, при которой время регулирования не превысит заданного значения. Если при начальном рассогласовании go ускорение регулируемой координаты ограничивается значением w, то частота среза не должна быть больше Осрг. т. е.

(5.39)

СР2 = К W/go.

Частота среза Юсра соответствует оптимальному переходному процессу при допустимом ускорении w.

Таким образом, частота среза должна быть выбрана по одному из следующих условий:

сР

: COppi или (В

(5.40)

(Or.

3L to.

Чем больше Wcp, тем меньше время регулирования. Однако если С0ср2 <С fOcpi, то ©ср не должна быть больше сосра-В этом случае требование в отношении времени регулирования, возможно, не будет удовлетворено.

Среднечастотная асимптота желаемой ЛАЧХ проводится через точку соср с наклоном -20 дБ/дек. При большем наклоне

трудно обеспечить необхо-j, димый запас устойчивости

и допустимое перерегулирование.

Протяженность средне-частотной асимптоты устанавливается исходя из необходимого запаса устойчивости. Из этих же соображений выбирают ее сопряженнее низкочастотной асимптотой. Кроме того, сопрягакщую асимптоту следует выбирать так, чтобы характеристика (со) возможно меньше отлича-Рис. 5.24 - лась от Lo ( ) и коррек-