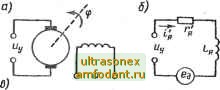Рис. 2.31

И в изображениях Лапласа (s) = knUJs +1); Wf (s)=

На рис. 2.30, г изображена структурная схема генератора. Математическая модель генератора представляет собой по возмущению пропорциональное звено, а по управляющему воздействию - апериодическое звено (первого порядка).

ДвигателЬо Принципиальная схема двигателя с независимым возбуждением приведена на рис. 2.31, а. При управлении со стороны якорной цепи напряжение возбуждения и = = const. На рис. 2.31, б приведена эквивалентная электрическая схема цепи якоря, где ги L - активное и индуктивное сопротивления обмотки якоря, i - ток якоря, e - э. д.с, наводимая в обмотке якоря при его вращении. Здесь делают такие же упрощающие предположения, что и при выводе уравнения генератора.

Запишем уравнение для цепи якоря:

(2.125)

Э. д. с. бд пропорциональна угловой скорости вала двигателя: бд = cffldt. Значение постоянной Cg зависит От тока воз-

буждения и конструкции двигателя. Уравнение (2.1,?5) с учетом последнего уравнения можно преобразовать к виду

Сз d<p 1

(T p+l)i + -p<P-iUy. (2.126)

где Т = LJra - электрическая постоянная времени цепи якоря.

На основе законов механики можно записать уравнение для моментов

, сРц,

У-рЧ = Мвр-Мс. (2.127)

где / - момент инерции вала двигателя (с учетом нагрузки); AJgp - вращающий момент; - момент сопротивления. Вращающий момент пропорционален току якоря:

M p-C4t. (2.128)

Значение постоянной с, как и Cg, зависит от тока возбуждения и конструкции двигателя.

Исключив из (2.126), (2.127) и (2.128) момент М и ток /и, получим

(Гя/ + 1)(--Л1с) + -РФ = 77- у-

Это уравнение можно преобразовать к виду

(Г Тир + Тр-{1)рч> = V My -Ада (TnP + l) Me, (2.129)

где Гам = JrJc - электромеханическая постоянная времени; = сз и Ад2 = г III с.- передаточные коэффициенты.

В изображениях Лапласа уравнение двигателя принимает вид:

(Тя T,s + rs-f 1) 5Ф (S) = kUis) - Ад2 (Г 5 + 1) Me(s),

(2.130)

где (/у (S) =L {Ыу}; (s) = L {М} .

Передаточные функции двигателя имеют вид: по управляющему воздействию

W (s) = ----

по возмущению (моменту сопротивления М) / ) дг(7яР+ )

W (S)= дг(7н5+1)

Структурная схема приведена на рис. 2.31, в, откуда видно, что математическая модель двигателя может быть представлена: по возмущению - в виде последовательного соединения форсирующего, колебательного (или двух апериодических, если < 2VT Тэм) и интегрирующего звеньев, а по управляющему воздействию - колебательного (или двух апериодических, если Т < гКТяГзм) и интегрирующего звеньев.

Усилитель, сравнивающее звено, делитель напряжения.

Эти элементы описываются уравнениями

Ыу = у8;. 8 = Мо- д. Мд = йдМг. (2.131)

где ky - коэффициент усиления усилителя; - коэффициент деления делителя.

Линеаризованное уравнение генератора связывает отклонение с внешними воздействиями ф и /. Поэтому небходи-мо преобразовать систему уравнений (2.131), так, чтобы она зависела от отклонения Аы (а не от и).

Запишем последние два уравнения системы (2.131) следу-щим образом:

Е=ио + Д о-( д.н + Д д); д.h-Л д = Йд( г.н+.Л г), (2.132)

где Он. д.н - номинальные значения задающего воздействия и напряжения делителя, определяемые равенствами

д.н = *я г.н; он = я.н- (2.133)

Уравнения (2.132) с учетом (2.133) можно записать так:

АЫд = йд Д г; 8 = Аыо - Д д.

В изображениях Лапласа уравнения усилителя, сравнивающего устройства и делителя напряжения принимают следующий вид:

Uis) = kE{s); £(8)=С/о(8)-/д(5); U{s)kUAs), где £(s)=L{6}; Uo{s)L {Ащ}; t/д(s) = L{ДМд}.