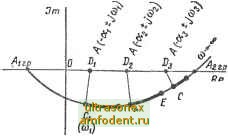3 (Шз)

Рис. 4.17

Удерманом введено y, /j

понятие годографа затухания [9].

Годографы затухания - линии постоянной частоты ю = const и переменного затуха- {(о=о) ния а = var в плоскости варьируемого параметра А, т. е, годографы затухания - это отображения линий, перпендикулярных мнимой оси в плоскости корней s, а так как кривая D-разбиения является конформным отображением мнимой оси на плоскости параметра А то годографы затухания ортогональны кривой D-разбиения (рис. 4.17). irp, -агр - это отрезок устойчивости.

Из точек Ci, Са и Cg (на кривой D-разбиения) проведены три годографа затухания до пересечения с отрезком устойчивости в точках Di, Dg и Dg. В точке характеристическое уравнение имеет в числе прочих пару комплексно-сопряженных корней Si,2 = - 1 ± /®1 при А = Ai. В точке при А = = Az корни Si,2 = - 2 ± /а>2- В точке Dg при Л = Лд корни Si 2 ~ -3 dz /®д- Таким образом, можно построить доминирующие ветви корневого годографа при изменении значения параметра Л.

В [9] показано, что для определения величины а в точках пересечения годографа затухания с отрезком устойчивости нужно оценить отрезок кривой D-разбиеиия CiE = CD в единицах частоты. Тогда щ -а !. Аналогично посту-

пают для точек Da, Dg и т. д.

Для построения корневого годографа нужно в (4.42) заменить S на (-а + /со):

Л (-а + /со) = -S (-а + /со) ? (-а + /со). (4.43)

Используя разложение в ряд Тейлора для полиномов S (-а + /со) и R (-а + /со), (4.43) можно представить [9] как

Л(-а + /ш) =

В (а) - - В (а) + -1 В(4) (а) + ... V 2! 41

+ /со

й(а)+ - В(3)(а)-...

С (а)-- С (а) +

+ /с0

-С(а)+-С (а)-...

. (4.44)

где В (а) = S (-а); С (а) = R (-а); В (а) =i dB (a)/da;

C(a) = rfC(a)/da; В {a) = d В {a) I da?; C {a)dC{a)/da?.

Чтобы определить действительные корни характеристического уравнения D (s) = О, нужно использовать (4.44) при ft) = 0.

Пример 4.3. Дана передаточная функция разомкнутой системы W (S) = + sTi) (1 + sT) (1 + 5Гз)].

где 1 = 0.1 с; = 0,2 с; = 0,3 с.

Варьируемый параметр в данном случае k. Характеристическое уравнение замкнутой системы

D (S) = (1 + sTy) (1 + sT) (1 + вГз) + й = 0.

Уравнение кривой О-разбиения (рис. 4.18) в плоскости k

= -(I + /соГх) (1 + /<оГ,) (1 + /<оГз).

В соответствии с (4.44) запишем выражение для k (-а + /ш):

*(-аЧ-/й)) = [A(s)l5 = -[ooSM Од г + 025 + Оз] <, =

-В (a)-f.

В(з> (а)

где 0 = 71 ГГз = 0,008; а,= (Г, Г + Гг Гз + Т ! Гд) =0.14;

аг = 1+72+7з=0.7; а=1, б (а) = А (-а) =ао а, а*-aj,-fi (а) =30-0 о-2а, а + а; В (а) =6оо а-2ai; В (а) = 6а. Тогда

А(-а + /(о) =

Оо а-Я) + 02 -оз+-(боо а -2oi)

- Зоо 2 + 201 -02+

= [0,008аЗ о, 14а2+0,7а-

- 1 + и (0,024а -0,14)]+ /{0 [-0,024а2+ 0,28а-0,7+0,008ш2].

Если принять а = О, то получим уравнение кривой £>-разбиения

Проведем из точки Су, соответствующей частоте <о = 4, годограф затухания до пересечения с отрезком устойчивости (-1 11,25).

В точке О, определим значение k = 1,8; osj = 5,5 - 4 = 1,5.

Аналогично, для годографа затухания из точки = 7,5;

2 = 8,6 - 8 = 0,6 и т. д. (рис. 4.18, а).

/7л 5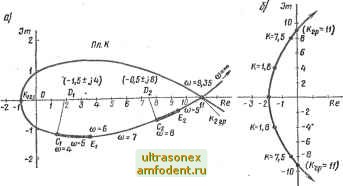

€о. = 0

Рис. 4.18

Вычислим значения к, принимая а= 1,5 и <о= 4 (точка DJ; ct = 0,7 и <о = 8 (точка D. При этом получим значения ki и k, близкие к рассчитанным выше.

Чтобы определить корни характеристического уравнения D (s) = 0, подставим в выражение для k (-а -)- /<о) значение <о = 0.

По полученным данным можно построить доминирующие ветви корневого годографа (рис. 4.18, б).

Можно отметить, сравнивая рассмотренные методы, что метод Ивенса требует меньше времени для вычислений, чем метод Удермана, не требуюш;ий поиска. Существуют и другие методы построения корневых годографов, например с использованием логарифмических частотных характеристик. Аналитические методы постр(№Ния требуют использования вычислительных машин для расчетов, но дают высокую точность.

Построение корневого годографа - это только первый этап анализа или синтеза автоматического регулирования. Как было упомянуто в начала параграфа, по корневому годографу можно судить о качестве регулирования (о реакции системы на типовое воздействие) и о выборе необходимых корректирующих устройств.

Задаваясь значением варьируемого параметра системы, можно вычислить ее переходную характеристку h {t), используя формулы разложения Хевисайда.

Для случая простых (некратных) корней переходную характеристику вычисляют по формуле (4.15), которую можно записать в более удобной для вычисления форме [9]. Запишем характеристический полином системы D (s) (4.15) в виде произведения двучленов: D (s) == (s - {s - ... {s - Sn), где