поненту exp (А), входящую в решение х (t) = ехр (At) Хр однородной системы х = Ах.

Алгоритм построения процессов с равномерным шагом h имеет вид

4+L=nk, k~0,,2,..., . (6.29)

При использовании матрицы порядок ошибки составляет - О фг -).

Так, при введении матрицы Di порядок погрешности О (ft) соответствует методу Эйлера, при введении матрицы Dg соответствует методу Эйлера-Коши, т. е. -О ф.), при использовании матрицы D4 - методу Рунге-Кутта четвертого порядка, т. е. порядок погрешности составляет О ф,).

При построении процессов в однородной системе с прогрессивно увеличивающимся шагом алгоритм имеет вид

Xft = D* Xo, (6.29а)

где Хо - вектор начальных условий.

Таким образом, в матричных критериях, основанных на построении и исследовании функционально-преобразованных матриц, заложены возможности не только анализа устойчивости, но и построения переходных процессов, удовлетворяющих заданным начальным условиям. В определенной степени трудоемкость компенсируется увеличением полезной информации.

Алгоритм позволяет анализировать устойчивость нестационарных систем прямым построением процессов, а также выявлять временную работоспособность системы на конечном интервале времени. В нестационарных системах функционально-преобразованная матрица перестраивается на каждом шаге. Алгоритм построения процессов в однородной нестационарной системе имеет вид

Xft+l = I>m(ft)Xft,

где Dm (ft/i) - функционально-преобразованная матрица, формируемая на каждом шагеЛ в соответствии с изменением исходной матрицы А {kh).

Выбор шага h осуществляется по радиусу /? круга, охват тывающего все собственные числа матрицы А. Величина h = 1 ? является шагом интегрирования, она может изменяться в широких пределах, при этом основным условием является нахождение всех собственных чисел матрицы внутри круга радиуса R. Таким образом, увеличивая длину шага, мы можем ускоренно строить переходные процессы, при этом вычисли-

тельная устойчивость сохраняется и качественная картина процессов, несмотря на рост погрешности, не изменяется.

Рассмотрим примеры, иллюстрирующие применение алгоритмов.

Пример 8.2. Рассмотрим систему dxjdt -

dx/dt ~ - 5xi - 2jCg.

Начальные условия (0) = I; (0) = 0,5.

Требуется найтн решение, которое определяет собственное движение (устойчивость) снстетйы. В качестве матрицы выберем матрицу

Матрица А и вектор начальных условий Xq имеют вид

Круг радиуса R= с А , где А - норма матрицы, примем равным 10. Шаг h = \IR = 0,1. Если шаг принять равным h = 0,01 (R = = 100), то масштаб времени уменьшается и потребуется большее количество вычислений. При Л = 0,1 матрица имеет вид

,Е--АЛ+ 0,01

(А/г2)

5 -2 10 -!

(АА)з (АЛ)

3! 0.001 6

10 -1 5 12 \ 0,97668 0,08988 -0,44941 0,796919

0,0001 24

5 12

-60 -19

Для получения решения можно использовать любую из формул

Xh+J = D4Xft и ли Xft = Dt Хо. Решение в момент времени t - kh =- 0,1 с имеет внд

хд,= х(0.1)=

В момент времени t - 0,2

Х2=х(0,2) =

0,99322 -0,49973

и далее

0,92514 -0,84461

Х4 =

0,82766 -1,00442

Х5 =

0,71808 -1,17239.

Решение системы приведена на рис. 6.3.

-0,5

Рис. 6.3

Пример 8.3. Рассмотрим однородную нестационарную систему х=А (/)х,

-5 1 --1 -Ш

А (/) =

Вектор начальных условий

.0,5

Требуется построить решение системы на промежутке 0; 1] секунд, используя функционально-преобразованную матрицу {kh).

- . Положим Л = О, I. При k = I

Рис. 6.4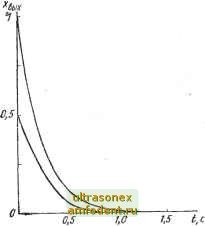

имеем

D2(Wt)=E-f A(feй)A-

-0,5 0,1

-0,1 -0,1. 0,12 -0,03

.0,03 6 . ~

0,62 0,071

~ -0,07 0,9 ]

Выполним вычисления в соответствии с алгоритмом:

1, 2.....