< <р < 0,7 с; 20% < о <

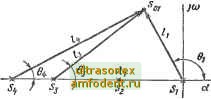Рис. 5.2!

Подставляя в (5.36) ij, = = 0,5 и а = 0,2, получаем

0 = 6; е-8 /°=0,2; <0о=П,2.

Наносим на комплексную плоскость (рис. 5.21) определяющий полюс Soi = - 6 + + /11,2 и полюсы неизменяемой части системы Sj = 0; Sg = - 10; Sg = - 20. Вводим дополнительный нуль = - 10, который скомпенсирует ближайший к мнимой оси полюс 2 неизменяемой части системы.

Введем еще дополнительный полюс так, чтобы полюс Soi находился на траектории корней скорректированной системы. Для этого по уравнению фаз определяем угол 6 наклона вектора 4, т. е.

04=180° -(61+63) = 180°-(П8° + 39°)= 23°.

Подсчитаем, какому значению передаточного коэффициента k соответствует точка траектории корней скорректированной системы (4.37):

k = hlsljisss) = l2,6-17,8-28,55/(20-26,4) = 12.

Значение k удовлетворяет требованиям; следовательно, вводить диполь не требуется.

По значению нуля Ki и полюса s4 определяем передаточную функцию последовательного корректирующего устройства:

W(s) =ft (0,ls-M)/(0,042s+l).

При этом передаточная функция скорректированной системы Wg (S) = 12/[s (0,05s + 1) (0,O42s+ 1) + 12] = = l/(0,000175s3 + 0,00767 + 0,0833s + 1) = l/[(0,029x Xs + 1) (0.0061 ls2 + 0,54s + I)] = 5650/!(s + 34,5) (s + 9s+ 164)].

Переходная характеристика системы

-34.5(

A(f)= 1-0,157 e

+ l,14e- X X sin (12/-2,ЗП

изображена на рис. 5.22. Она имеет следующие показатели качества: = 0,635 с и 0=27 % Итак, при выбранном последовательном корректирующем устрой-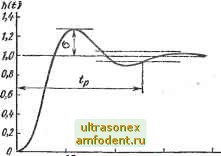

O.S Рис. 5.22

стве система удовлетворяет требованиям. Однако следует заметить, что показатели качества скорректированной системы заметно отличаются от тех значений (tp = 0,5 с; а = 20 %), по которым производится расчет. Это объясняется недостаточным удалением полюсов Sg и (см. рис. 5.21) от определяющей пары комплексно-сопряженных полюсов. В результате полюсы скорректированной системы имеют следующие значения: s = - 4,5 ± /12; Sg = - 34,5 т. е. пара комплексно-сопряженных полюсов отличается от выбранной (определяющей) и на динамику системы оказывает влияние полюс Sg.

§ 5.7. Синтез корректирующих устройств по логарифмическим амплитудно-частотным характеристикам

Рассмотрим еще один метод синтеза корректирующих устройств, весьма детально разработанный и нашедший широкое применение.

Пусть передаточная функция неизменяемой части системы o(s)-feo?o(s)/[s°Qo(s)l.

где Ro (s); Qo (s) - полиномы от s со свободным членом, равным единице; ко, Vo - постоянные величины.

Потребуем, чтобы система была астатической v-ro порядка, имела добротность k, перерегулирование не более о и время регулирования не более tp. Такой комплекс требований весьма часто предъявляют к следящим системам. Значения порядка астатизма v и добротности k выбирают, исходя из необходимой точности регулирования в установившихся режимах. Выбором показателей качества переходной характеристики - перерегулирования а и времени регулирования - гарантируются необходимые быстродействие и динамическая точность системы.

В некоторых случаях необходимо, чтобы при начальном рассогласовании go ускорение регулируемой координаты ке превышало некоторого допустимого значения w. Такое ограничение необходимо, например, в механических системах, когда регулируемой координатой является перемещение. Предупреждается появление в регулируемом объекте и в исполнительном элементе недопустимых перегрузок (механических, электрических и т. п.).

Легко установить, что если порядок астатизма Vq неизменяемой части системы меньше v, то в усилительно-преобразо-

вательном элементе необходимо иметь (v - Vo) интегрирующих звеньев. Так же легко определяется необходимое значение передаточного коэффициента преобразовательно-усилительного элемента, равное klkf,.

Задача сводится, следовательно, к синтезу корректирующего устройства, обеспечивающего необходимые динамические свойства системы. При этом будем полагать, что передаточная функция неизменяемой части системы

.lFo(s) = fe/?o(s)/IsQo(s)l, (5.37)

так как уже выяснено. Какой передаточный коэффициент должен иметь усилительно-преобразовательный элемент и нужны ли в нем интегрирующие звенья.

Метод синтеза корректирующих устройств, разработанный В. В. Солодовниковым [81, основывается на соответствии между логарифмическими частотньши характеристиками разомкнутой системы и ее статическими и динамическими свойствами в замкнутом состоянии. Метод используется для систем минимально-фазового типа, и поэтому достаточно рассматривать лишь логарифмическую амплитудно-частотную характеристику разомкнутой системы.

Построение ЛАЧХ неизменяемой части системы. Асимптотическую ЛАЧХ Lo (to) нужно строить по передаточной функции Wo (s), определяемой (5.37). Предварительно каждый из полиномов /?о (s) и Qo (s) передаточной функции Wo (s) следует разложить на множители вида (TjS + 1) и (77s + 27s + 1), где К 1.

Разложение это удобно осуществлять итерационным методом, предложенным О. М. Крыжановскнм. Изложение метода с примерами его применения дано в [91.

Пусть имеется полином третьей степени G (s) = + aif + ajs + 1 = йо (s + cs -\- cs + с),

где Ci = fli/ao; = Vo и = l/йо.

Вычисляем: 1 = cjci pi = (c - Oi); = cjic - pi); = 2 (Ct, - а); 3 = Сз/(С2 - P); Рз = з (c - Юд) и т. д.

Если процесс сходящийся, т. е. с увеличением i значения щ ,и рг стремятся соответственно к некоторым пределам а и р, то

С (S) = (s/a + 1) (aflos* + Рйо s + 1).

Процесс вычисления щ и Pf может оказаться расходящимся. Тогда нужно делать такие вычисления:

a, = ca/ci-Cg/cf; a2 = C2/(i;i-а,)-<;з/(<;1-а ; 3 = с/(С1 - г) - f з/(<7, - а) и т. д.