печатаются координаты точек, расположенные в вершинах квадратов внутри (или вне) области.

Для более экономичного слежения по контуру может быть использован видоизмененный алгоритм. Одно из возможных изменений заключается в следующем. Брли при обходе контура области по квадратам искомая граний:а области не пересекается в течение двух последовательных шагов, то надо окружать то место где произошло последнее пересечение, и впредь до нового пересечения повороты делать после каждого нечетного шага, причем шаг, на котором было последнее пересечение, следует считать нулевым. Таким образом, изменение на плоскости параметров происходит по квадрату с удвоенной

Вход в область - поборот ло часоЗой стрема Выход из области-подорот против часодой стрелка

Рис. 6.10

стороной. Повороты, как и прежде, выполняются в соответствии с правилом: вход в область - поворот по часовой стрелке; выход из области-поворот против часовой стрелки. Правило поворотов при пересечении границы искомой области иллюстрируется на рис. 6.10.

Алгоритм обхода по вершинам прошел достаточную практическую проверку и, несмотря на усложненную логику, оказался экономичным. Он легко программируется, при обходе выполняется относительно небольшое количество лишних шагов. Замкнутая область сложной конфигурации с перегибами и крутыми поворотами отслеживается этим алгоритмом без срывов.

Можно применить более точный способ движения по границе искомой области ( гусеничный метод).

Принцип слежения сводится к повороту и параллельному переносу координатных осей. Слежение вдоль границы области состоит в последовательном продвижении вдоль границы с ппмлшью поступательных перемещений и поворотов. -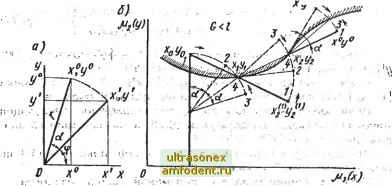

Рйо. 6.11

Пусть HMeiptpH две точки [ху, и [х, yj, принадлежащие искомой области на плоскости параметров ЦгИа. и пу(;ть интересующая нас область лежит справа от прямой, соединяю-; щей точку [jCi, Уу] с [х, у]. Тогда приближенно можно указать следующую точку по формулам

xo = 2Xi - ху, = 2у

Геометрически это означает, что сделан шаг по прямой, соединяющей точки \ху, уу] и [х, yl, от точки [ху, уу] к точке [ха, у], равной расстоянию между этими точками (рис. 6.П,о, б).

В полученной точке с координатами 1лг°, у°] вычисляется функционал G (jc , У°]. При этом возможны два случая:

I. G уП~1> 0.

Анализируемая точка с координатами Ы, if] находится вне искомой области. Тогда выполняется поворот против часовой стрелки и производится определение положения новой точки \х, уЦ по формулам

х = Ха + [х<-Xjlcostto-i/alsinao; 1

, S=S2 + [: °--alsinao + Ii/i/alcosao, I

(6.76)

где a - угол поворота. 2. GU . уЧ-КО.

Точка находится внутри искомой области. Для выхода на границу осуществляется поворот по часовой стрелке. Положе-