

 |
 |
|
Главная страница Векторные методы процессов Продолжение габл. 4.2 0.50 0,55 0.60 0,65 0.70 0.75 0.80 0.85 0,90 0.95 1.00 0,996 0,997 0.9 0,999 1.0 1,000 1,000 1.000 1,000 0,996 1.000 1,001 1,002 1,002 1,002 1,002 1,002 1 002 1,000 1,004 1,006 1,007 1,008 1,006 1,004 1,002 1,000 0,997 1,000 1,001 1,002 1,003 1,003 1,003 1,002 1,001 0,997 0,996 0,997 0,998 0,999 1,000 1,001 1.002 1,002 0,99L 0,992 0,994 0,997 1,000 1,002 1,003 1,004 1,004 0,991 0,998 1,002 1,007 1,008 1,008 1,005 1.004 1,002 0,997 1,008 1,015 1,017 1,017 1,014 1.008 1,001 0,987 1,012 1,022 1,025 1,023 1,015 1,005 0,991 0,986 0,984 1,024 1,028 1,027 1,023 1,012 0,995 0,985 0,978 0,977 1,029 1,026 1,016 1,002 0,998 0,979 0,975 0,977 0,983 lg (M-P(a>)--/Q(co) = u + jv Pico) l + u + iv (3((0)== (l+u-jv) (u + jv) 0+u)+v (P - l)u + i2P-l)u + iP - l)ir + P = 0; (4.85) + 2Qu + Qv - v + Q 0. (4.86) Кривая (4.85) является окружностью, центр которой Р .= = const лежит на оси абсцисс, так как уравнение не содержит v; окружности имеют общую точку и = О, и == I, и == - -Р(1 - Р). Радиус окружности /? = 0,51-Р!. (4.87) Соответствующие кривые показаны на рис. 4.36 с указанием значений Р, для которых эти окружности построены. Аналогично находят все ок- ружности Q = const (рис. 4.36). Радиус окружности R = 1/[21<21]. (4.88) На круговую диаграмму накладыйают кривую W (/(о), выполненную в том же масштабе, и считывают значения Р (to,-), которые 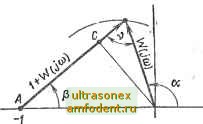 О Re W(jta)
соответствуют индексам окружностей сетки, пересекающей кривую W (/со) в точках, соответствующих частотам со. Вещественную частотную характеристику определяют по логарифмическим частотным характеристикам. Передаточную функ15ию разомкнутой системы можно записать через амплитуду и фазу: Й7(/со)=Л(со)е/1< ) = Л(со)[сс5ф((о)+/ыпср(из)]. (4.89) Если (4.89) подставить в (4.83) и разделить вещественные и мнимые части, то ((О) + А (ю) cos ф (оз) Я(со) = (со) -\-2А (со) cos ф (со) + I А (со) sin ф (со) A2(u))-f 2Л ((й)со8ф(й))-Ь1 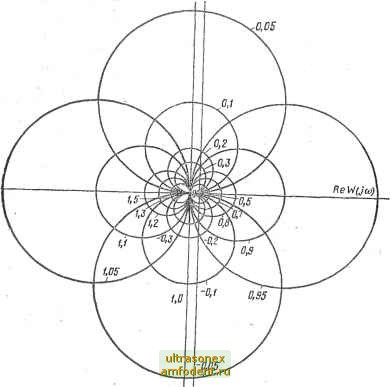
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |