По этим формулам построены номограммы для определения Р (со) и О (ю) по логарифмическим частотным характеристикам. Эти номограммы построены на плоскости, по оси абсцисс которой отложены значения (р, а по оси ординат - 20 Ig А (стороны квадрата). На эту плоскость накладывают ЛАФЧХ разомкнутой системы с указанием частоты. Значения вещественной частотной (или мнимой) характеристики определяют по точкам пересечения нанесенной кривой ЛАФЧХ с кривыми номограммы. Эти номограммы представлены на рис. 4.37.

, дБ f, град

-o2D -3D0 -2SD -260 -2йО -220 -200 -1дО -Ш -Ш -120-Ш -80 -ВО -- 5 Lm.dE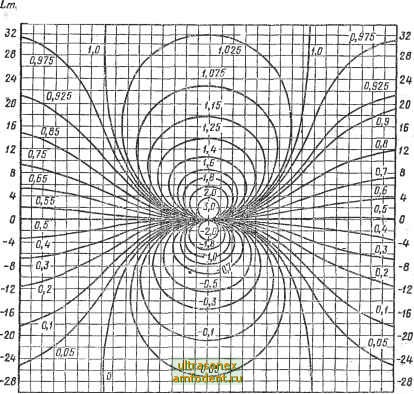

-320 -300 -280 -260 -20 -220 -200 -160 -1Б0 lUO -120 -100 -80 -60 -W

f, град

Оценка качества по показателю колебательности. Определение показателя колебательности М приведено в § 4.4. Если АЧХ системы при нулевой частоте равна 1 (Лз (0) = 1), то показатель колебательности

М = Лз шах (со) - 7 (/СО)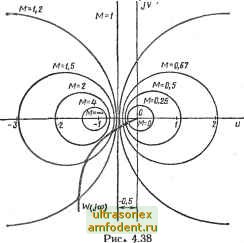

1 + U7(ia>)

Чтобы определить показатель колебательности системы,

можно воспользоваться амплитудно-фазовой частотной характеристикой разомкнутой системы W (/(о) = ы (со) -f- jv (со), где ы = Re 1Г (/со), V (со) = Im 1Г (/со).

Показатель колебательности можно вычислить так:

шах V[+ (to)] + t;2(u))

l+ (tu) + it;(to)

Возведя в квадрат обе части равенства, получим

{[1 + и (со)Р Л- v (со)} = 2 (со) + хР- (со).

После алгебраических преобразований можно записать

[ы (со) + MV(M- 1)] + (со) = 7И V(M -1) (4.92)

Выражение (4.92) является уравнением окружностиг с радиусом R = М1{М - 1) и с центром, смещенным от начала координат влево на величину С = M?}{JM - \\. Задаваясь различными значениями М от О до оо, можно построить семейство таких окружностей (рис. 4.38). При М = 1 окружность вырождается в прямую (/? оо, C-s- оо), параллельную мнимой оси и проходящую через точку (-О, 5, /0):

lim (С -R) = lim \М1{М - 1) -МЦМ- 1)1 = 0,5.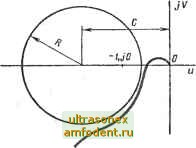

Рис 4.39

При О <. М <. \ окружности располагаются справа от линии, соответствующей М = 1, а при Mz> i - слева от нее. Если М- сю, то окружность вырождается в точку с координатами [-1, /0]. Номограммы можно использовать для построения амплитудно-частотной характеристики замкнутой системы Л 3 (со). Для этого на номограмму наносят амплитудно-фазовую характеристику разомкнутой системы W (/(й), далее по точкам пересечения последней с окружностями определяют значения А(( ). Когда нужно оценить значение показателя колебательности М, то строить амплитудно-фазовую характеристику не нужно, а необходимо только оценить, какой наименьшей окружности она коснется; значение М = const, соответствующее этой окружности, и будет показателем колебательности.

При проектировании системы может быть поставлено условие, чтобы показатель колебательности М не превышал заданного значения. Это значение определяет ту запретную область, куда не должна заходить амплитудно-фазовая характеристика разомкнутой системы W (/со) (рис. 4.39). В том случае, когда М - I, систему автоматического регулирования можно рассматривать как колебательное звено. При этом передаточная функция замкнутой системы

(s)---.l/(l+2rs + 75).

60 1>0 20 О

30 20 Ю О

0,25 0.5 Рис. 4.40

0.75 1Р i

TjO %2S hS t.7S 2,0 M Рис. 4.41