G% М

/ /,; U2 и и (о)

U),tp

ж Зж 2х

1 1,1 1,2 и 1Л Р(0)

Рис. 4.30

наклон к = cOi/coa. Функция, соответствующая частотной характеристике Б (рис. 4.31), записывается так:

1 при 0<со<и;

Р(со)= 1 -(ш-и)/(1-к)=(1- )/(!-к) при к<со<1;

О при со <: О и со > 1.

Если принять такую единичную трапецию за некоторую вещественную частотную характеристику, то соответствующая ей переходная /i-функция определяется интегралом:

h{x) =

sin от

dco +

1-<о) sin (ОТ

(1-х)

п (1-к) L 1

. , , Г sin сот где Si (т) = ---

Si (%) - и Si {%%) +

cos Т -cos XT

(4.79)

do)-интегральный синус.

Значения /i-функций даны в табл. 4.2. Р

Для трапеции с другой высотой Pji, основанием со и точкой излома coi = исоа (характеристика А на рис. 4.31) получим (по свойствам 2 и 3 об изменении масштабов) q

hj, (О = Pnh (т/соа), (4.80) где / = т/сог.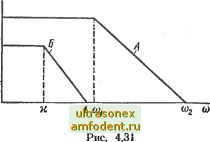

Обычно поступают так: сначала характеристику Р (со) приблизительно разбивают на прямолинейные отрезки, при этом в окрестности экстремумов прямолинейные отрезки располагаются параллельно оси со (рис. 4.32, а). Далее из точек изломов проводят линии так, что характеристика оказывается разбитой на несколько трапеций, частично наложенных одна на другую. Затем эти трапеции вычерчиваются на другом чертеже таким образом, чтобы основание каждой из них легло на ось со (рис. 4.32, б).

Для всех трапеций определяют hi (ti), по (4.80) - соответствующие им hi (t); вычерчи-вак/г кривые на одном графике; их знаки должны совпадать со знаками ординат соответствующих трапеций. Суммируя графически вычисленные процессы (рис. 4.32, в), получим h (t) - = hi (0.

Можно также характеристику Р (со) представить линейными отрезками, но распределить их с лучшим приближением к кривой и тогда пользоваться методом треугольников, предложенным А. А. Вороновым [2]. Полученные при пересчете значения ti из по (4.80) могут не совпадать для отдельных трапеций, поэтому при,использовании метода трапеций возникает необходимость графического суммирования составляющих кривых Л,- (О, что ухудшает точность результатов. От этого недостатка свободен метод треугольников.

Представим характеристику Р (со) линейными отрезками (рис. 4.33), обеспечив возможно лучшее приближение к кри-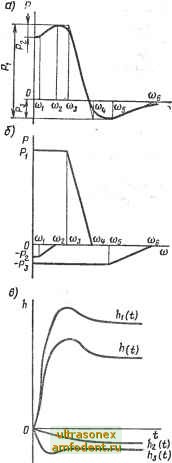

Рис. 4.32

вой; отрезки продолжаем до пересечения с осью ординат, при этом площадь под кривой будет разбита на пять треугольников: АОВ, BCD, DEF, FGH, GHK. Затем каждый из треугольников заменим другим с основанием, равным проекции основания данного треугольника на ось со, с высотой, равной стороне, лежащей на оси Р. На рис. 4.34, а, б показана замена /\рВС .на Л!!! так, чтобы ОА = OA w ОВ = BD. ; Из (4.79) при к = О

ft(x)=A(siT-l=) (4.81)

определяют значения Л-функции для единичного треугольника ( 1 = i = 1).

Соответствующие значения /г-функции даны в табл. 4.3. Заметим, что переходный процесс для, треугольной частотной характеристики описывается монотонной функцией р времени. Для того чтобы р показать это, продифференцируем (4.81):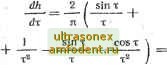

= -i-(i-cosT). (4.82) пт

Из полученного выражения видно, что производ-на.я h (т) положительна и обращается в нуль при значениях т = 2kn, где А; = О, 1, 2, ...

Переходный процесс для треугольников, замещающих Р (а), определяют из следующей зависимости: Xk {i)==Phh (t/co,J, где Ph - высота; со - основание замещающего треугольника.

Ркс. 4.33