Пример 2.1. Проиллюстрируем изложенное на примере звена, описываемого уравнением (2.1). Пусть заданному режиму соответствуют

и = Н.; н = н*; / = /*; у=у*\ у = у*\ У=У*. (2.3)

Обозначим отклонения реальных значений и, f к у от требуемых через Аи, Д/ и Ау, т. е. Аи = и - и*, Д/ = / - /*, Ау ~ у - у*. Тогда и = и* + Аи; и ==и* + Аи; f = f* -\- Af; у = у* -\- Ay; у = = у* -\- Ау; у = у* + Ау. Подставим эти выражения в (2.1) и, рассматривая F как функцию от независимых переменных и, и, у, у и у, разложим ее в ряд Тейлора в точке (2.3) и отбросим малые члены более высокого порядка, чем отклонения. Тогда (2.1) примет вид

F* + (дР/ду)* Ау+ {дР/др* Ау+(дР/ду)* Ау+ (дР/ди)* Аи +

-\-(дР/ди)* Au+f*-\-Af = 0. (2.4)

Здесь звездочка сверху обозначает, что соответствующие функции и производные вычисляются при значениях аргумента, определяемых соотношениями (2.3). Когда в системе устанавливается заданный режим, уравнение (2.1) принимает вид f * + /* = 0. Вычтя это урав-ние из (2.4), получим искомое уравнение звена в отклонениях:

aoAy + Oi Ау-\-а2 Ау-Ь Аи - Ь Аи-Са А/ = 0, (2.5)

тле ао={дР/дуГ; а=={дР/ду)*; а=={дР/ду)*;

Ьо=- {дР 1ди)*; bi=- {дР/ди)*; Со = - 1.

Если время / явно не входит в исходное уравнение (2.1) и, кроме того, заданный режим является статическим - величины у*, и* и /* не зависят от времени, то коэффициенты линеаризованного уравнения (2.5) являются постоянными.

Звенья и системы, которые описываются линейными уравнениями, называют соответственно линейными звеньями и линейными системами.

Уравнение (2.5) было получено при следующих предположениях: 1) отклонения выходной Ау и.входной Аи величин достаточно малы; 2) функция F обладает непрерывными частными производными по всем своим аргументам в окрестности точек, соответствующих заданному режиму. Если хотя бы одно из этих условий не выполняется, то линеаризацию производить нельзя. По поводу первого условия необходимо отметить следующее: нельзя раз и навсегда установить, какие отклонения считать малыми. Это зависит от вида нелинейности.

Часто нелинейную зависимость между отдельными переменными, входящими в уравнение звена, задают в виде кривой. В этих случаях линеаризацию можно произвести графически.

Геометрически линеаризация нелинейной зависимости между двумя переменными (рис. 2.2) означает замену исходной кривой А В отрезком ее касательной АВ в точке О, соответствующей заданному режиму, и параллельный перенос начала координат в эту точку.

В зависимости от того, входит или нет время явно в уравнение, системы разделяют на стационарные и нестационарные. Автоматические системы управления стационарными, если они при постояннвгх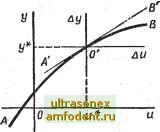

Рис. 2.2

(звенья) называют внешних воздействиях описываются уравнениями, не зависящими явно от времени. Это означает, что свойства системы со временем не изменяются. В противном случае система называется нестационарной. Для линейных систем можно дать также следующее определение: стационарными линейными системами (звеньями) называют системы (звенья), которые описываются линейными уравнениями с постоянными коэффициентами; нестационарными линейными системами (звеньями) или системами с переменными параметрами - системы (звейья), которые описываются линейными уравнениями с переменными коэффициентами.

§ 2.2. Основные свойства преобразования Лапласа

В этом параграфе даны основные сведения о преобразовании Лапласа, которые будут использованы при рассмотрении систем, описываемых линейными дифференциальными уравнениями.

Преобразованием Лапласа называют соотношение

X(s)= х(Ое- Л.

ставящее функции х (f) вещественного переменного в соответствие функцию X (s) комплексного переменного s{s = а-{-+/©). При этом X (t) называют оригиналом а X (s) - изобра-

жентм или изображением по Лапласу. То, что х Ц) имеет своим изображением X (s) или оригиналом X (s) является х (), записывается так:

x(t)X is) или Х (s) == X (t).

Иногда также пользуются символической записью

X (S) = L {X (t)},

где L - оператор Лапласа.

Предполагается, что функция х (t), которая подвергается преобразованию Лапласа, обладает следующими свойствами: X (t) определена и кусочно-дифференцируема на всей положительной числовой полуоси [о, оо]; х (f) =0 при / <; 0; существуют такие положительные числа Мне, что д; () Же* при О <; с . Функции, обладающие указанными тремя свойствами, часто называют функциями-оригиналами. Соотношение

2щ J

Со-/оо

X{s)etds,

определяющее по известному изображению его оригинал (в точках непрерывности последнего), называют обратным преобразованием Лапласа. В нем интеграл берется вдоль любой прямой Res == Oq > с. Символически обратное преобразование Лапласа можно записать так:

x{t)L- {X{s)},

где символ - обратный оператор Лапласа.

Остановимся на основных свойствах преобразования Лапласа.

1. Свойство линейности. Для любых постоянных аир L {ах (t) + (t)} = aL {х, (t)} + pZ. {х (t)}.

2. Дифференцирование оригинала. Если производная х (t) является функцией-оригиналом, т. е. обладает указанными выше тремя свойствами, то L {х (t)} = sX (s) -х (0), где

X(s) = L {х (t)}, х{0) = lim х (t). Если п-я производная х (t} является функцией-оригиналом, то

L л;(0}=8 Л(8)-8 -л;(0)-s -zx(0)-X (0),

(ft) (ft)

где х{0) =limx (/), k = 0,l,...,n - l.

t-*-i-o