при начальном условии х = х определяется формулой Коши

X (О = X (t, to) + J X (t, т) [В (т) U (т) + С (т) f (т)] 4т. о

Эта формула позволяет определить решение неоднородного уравнения (2.113), если известна какая-либо система из п линейно независимых решений однородного уравнения (2.114).

§ 2.10. САР напряжения генератора постоянного тока. Математическое описание

Рассмотрим в качестве примера вывод дифференциальных уравнений и передаточных функций системы автоматического регулирования (САР) напряжения генератора постоянного тока, блок-схема которой приведена на рис. 2.29. Она состоит из электронного усилителя у, двигателя постоянного тока с независимым возбуждением Д, являющегося исполнительным элементом, генератора г (объекта регулирования) и делителя напряжения ДН, выходное напряжение Ыд которого в сравнивающем устройстве вычитается из заданного Uq. Определим сначала дифференциальные уравнения и передаточные функции отдельных элементов, входящих в рассматриваемую систему. Начнем с объекта регулирования.

Генератор. Управление генератора производится путем изменения переменного сопротивления включенного в цепь возбуждения (рис. 2.30, а). Обозначив через его номинальное значение, т. е. значение R, при котором ток в цепи возбуждения принимает номинальное значение г.ц, можно записать

Rn = Rn.n + AR.

Отклонение AR переменного сопротивления пропорционально углу ф поворота вала двигателя:

А/? = -С1ф. (2.115)

Здесь Ci - положительная постоянная, знак минус указьша-ет, что при повороте вала двигателя в положительном направлении сопротивление R уменьшается, в отрицательном - увеличивается. Таким образом, входной (управляющей) величиной генератора является угол ф, а выходной - падение

Рис. 2.29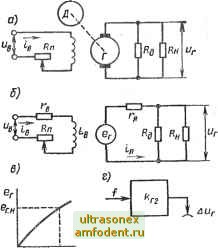

напряжения Ur на нагрузке.

Составим уравнение динамики генератора без учета влияния гистерезиса, вихревых токов и т. п. На рис. 2.30, б приведена эквивалентная электрическая схема генератора. На ней и Ljj - активное и индуктивное сопротивления обмотки возбуждения, вр - э. д. с. генератора, г - активное сопротивление обмотки якоря (его индуктивным сопротивлением пренебрегаем), - сопротивление нагрузки (нагрузка предполагается активной). Э. д. с. генератора связана с током возбуждения нелинейной зависимостью

er=F{h), (2.116)

Рис. 2.30

примерный график которой приведен на рис. 2.30, в. Дополнительное сопротивление /?д выбирается таким, что током через него по сравнению с током нагрузки можно пренебречь. С учетом сказанного можно записать: для цепи возбуждения

в = ( в + п.н + Щ >в + Lb dijdt; (2.117)

для якорной цепи

(2.118)

В статическом режиме при номинальных значениях токов возбуждений ig.h и якоря эти уравнения принимают вид

в. =( + /?п.н)1в. ; (2.119)

ег.н=(я + н.н)1н.н; г.нн.ня.к- (2.120)

Произведем линеаризацию в рабочей точке, соответствующей номинальным значениям токов возбуждения и якоря. Подставим в (2.И7) Гб = 1в.н + Д1в и выражение (2.U5). Отбрасывая малый член CiAifp более высокого порядка, чем Дв и ф, и учитывая (2.119), получим

или в символической форме

(Г,р-Ы) At = Й1ф, (2.121)

= LJir + . ); fti = сх i.j{r -f /? . ). Произведя линеаризацию (2.116), получим

ег=ег.н + С2А1 в, (2.122)

б = в.н

Используя это выражение для и уравнение статики (2.120), уравнения (2.118) можно преобразовать к виду

cz Aib = ( + 1 ) А , - Д? / . (2.123)

Исключив из (2.121) и (2.123) Aib, окончательно получим одно уравнение, связывающее входную (управляющую) ф и выходную Аыг величины и возмущение f = ArJ генератора;

(ГвР H)A p=ft,lФ-ft.-a{r,p-f 1)Л (2.124)

В изображениях Лапласа это уравнение принимает вид (Г, s+l)U, (s) = Art Ф is) + iT, s + l)F is),

где (/r is) = L(A r}; Ф (s) = L (ф); F (s) = L {/}. К генератору приложены два внешних воздействия (ф и /), и он описывается двумя передаточными функциями: передаточной функцией по управляющему воздействию и передаточной функцией Wf по возмущению. Для них имеем: в операторной форме

ip) = krx/iTp +1); Wfip) = k.