

 |
 |
|
Главная страница Векторные методы процессов тяц и вполне определенные три корня в комплексной плоскости корней s (рис. 3.22). Например, точке М, имеющей координаты ам, ам и Одм, соответствует полином Dm (s) = + aus + oAfS + ам, имеющий три корня Sim, sm и sm в плоскости корней (рис. 3.22, а). Другой точке, например N, имеющей координаты л/, aN и OsN, соответствует полином Dn (р) = + aNS + + aNS + OsN, корни которого SyN, и SsN и. т. д. При некотором значении коэффициентов уравнения (3.77) один из корней попадает в начало координат или пара корней попадает на мнимую ось, т. е. корни его будут иметь вид О или ± j(x)k и, следовательно, соответствующая точка в пространстве параметров будет удовлетворять уравнению D (/ ,) = (iar+a,Umr + Цщ) + а, = 0. (3.78) Этому уравнению при - оо < со < оо соответствует некоторая поверхность S, часть которой показана на рис. 3.22, б. При изменении ксвффициентов корни характеристического уравнения также изменяются и попадают на мнимую ось тогда, когда точка в пространстве коэффициентов попадет на поверхность S. При пересечении такой поверхности S корни переходят из одной полуплоскости корней в другую. Следовательно, поверхность S разделяет пространство коэффициентов на области, каждой точке которых соответствует определенное одинаковое число правых и левых корней. Эти области обозначают D (т), где т - число правых корней характеристического уравнения. Разбиение пространства коэффициентов на области с одинаковым числом правых корней внутри каждой области и выделение среди полученных областей области устойчивости называют методом £)-разбиения. Ct,H 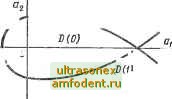 Для характеристического уравнения третьего порядка ---,.(0 * в пространстве коэффициен- тов можно наметить четыре области: D (3), D (2), D (1), \ о /\в(2; D (0). Последняя область D (0) будет областью устойчивости. Если изменяются не все ко- Рис. 3.23 эффициенты, а часть из них, например два-и при = const, то вместо поверхности получим линию, которая является сечением поверхности 5 плоскостью 3 = const. Эта линия разделит плоскость коэффициентов % - 2 на области с одинаковым числом правых корней (рис. 3.23). Для уравнений более высокого порядка (п > 3) вместо обычного трехмерного пространства получаются многомерное пространство и гиперповерхности, разбивающие это пространство на области, что сильно усложняет задачу, а рассмотрение теряет наглядность. Так как переход через границу D-разбиения в пространстве коэффициентов соответствует переходу корней характеристического уравнения через мнимую ось, то уравнение границы D-разбиения в общем случае =. (/О)) + %(/©) - -f ... + а = 0. (3.79) Из (3.79) видно, что уравнение границы D-разбиения мо-жет быть получено из характеристического уравнения систе-,мы заменой s = /со. Границу D-разбиения можно строить не Чолько в пространстве коэффициентов at характеристического уравнения, но и в пространстве параметров системы (постоянных времени, коэффициентов усиления и т. д.), от которых зависят коэффициенты характеристического уравнения. /J-разбиение по одному (комплексному) параметру. Предположим, что требуется выяснить влияние на устойчивость какого-либо параметра v, линейно входящего в характеристическое уравнение. Для этого сначала характеристическое уравнение приводят к виду D (S) = S (s) + vN (s) = О, (3.80) где S (s) - полином, не зависящий от v; N (s) - полином, содержащий V множителем. граница D-разбиения определяется уравнением D (/ю) = 5 (/ ©) + vN (/©) = 0, (3.81) откуда V = - 5 (j(i>)/N (/©) = X (ю) + /г (©). (3.82) Так как изменяемый параметр v в линейных системах является не комплексным, а вещественным числом (коэффициент усиления, постоянная времени и т. д.), то (3.82) следовало бы дополнить условием Y (со) = 0. Однако при первоначальном построении не будем делать этого ограничения и будем временно считать изменяемый параметр комплексной величиной v, отмечая это чертой сверху, чтобы отличить ее от вещественного значения v. Давая со значения от-оо до оо, можно по (3.82) вычислить X (со) и Y (со) и построить на комплексной плоскости v границу D-разбиения. При построении границы D-разбиения достаточно построить ее для положительных значений со и затем дополнить зеркальным отображением построенного участка относительно, действительной оси (рис. 3.24, б). Если при изменении со от - оо до оо в плоскости корней двигаться по мнимой оси и штриховать ее слева (рис. 3.24,й), то такому движению в плоскости v соответствует движение по границе D-разбиения, которую также щтрихуют слева по обходу при изменении со от - оо до оо (рис. 3.24, б). Если в плоскости пересекать границу D-разбиения по направлению штриховки (стрелка 1), то в плоскости корней один из корней переходит из правой полуплоскости в левую. Если же в плоскостил пересекать границу D-разбиения против штриховки (стрелка 2), то в плоскости корней, один из корней переходит из левой полуплоскости в правую. Если штриховка двойная (например, в точке пересечения кривых), то мнимую ось пересекают два корня. tco=>0 tcu<D 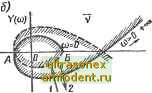
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |