Рис. 4.43

оЬщая часть для определения всех функций (t). Дополнительные блоки модели (рис. 4.43) реализуют операторы L% (р) и Ml (р), с общей частью они соединены переключателем П. Как видно из схемы рис. 4.43, функция чувствительности координаты X определяется последовательно во времени по всем параметрам. Для одновременного определения всех функций чувствительности по параметрам используем передаточные функции системы [13].

Выходная координата системы х (t) связана с задающим воздействием g (t) зависимостью

X (s)= W (s) G (s), (4.105)

где W (s) - К {s)/D (s) - передаточная функция системы; X (s) и G (s) - изображение по Лапласу выходной и входной величин.

Определим изображение функции чувствительности (s), дифференцируя (4.105) по а:

H,(s)

и,

X. (s) dlnW (s)

dW js)

X X(s)

W (s) aiTft (s)

(4.106)

где (s).- передаточная

функция элемента, параметром которого является а.

Обозначим общую часть ду через (s), тогда SlnW (S)

а для функции чувствительности можно записать U{s) = X(s)H,{s)H,(s).

U{s)=X{s)HAs)H%(s), где ЯИ8)-Я,(5)М..

На рис. 4.44 показана схема модели для одновременного определения функций чувствительности по параметрам Oj, .... .... czft. Рассмотренный метод позволяет упростить модель чувствительности за счет упрощения общей части модели, в частности общая часть может быть представлена пропорциональным звеном. Подобное упрощение модели используется в беспоисковых системах оптимизаций.

Глава 5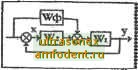

ОБЕСПЕЧЕНИЕ УСТОИЧШОСТИ.

ШВЬШЕНИЕ КАЧЕСТВА

РЕГУЛИРОВАНИЯ

И СИНТЕЗ ЛИНЕЙНЫХ

АВТОМАТИЧЕСКИХ СИСТЕМ

§ 5.1. Общие положения

Первой проблемой, которая решалась теорией автоматического регулирования, было обеспечение устойчивости автоматических систем. Позднее центральной задачей стало достижение необходимого качества регулирования. Систематизация и обобщение накопленных знаний привели к созданию методов научного проектирования (синтеза) систем с заданными показателями точности регулирования и быстродействия.

В настоящей главе излагаются основные сведения о способах и средствах улучшения свойств линейных систем автоматического регулирования. Затем рассматриваются наиболее употребительные методы их синтеза.

Проблема обеспечения требуемых свойств линейных автоматических- систем весьма сложна. В ней могут быть выделены прежде всего следующие частные задачи: обеспечение устойчивости (стабилизация); повышение запаса устойчивости (демпфирование); повышение точности регулирования в установившихся режимах (уменьшение или устранение статической ошибки воспроизведения задающего воздействия, уменьшение или устранение влияния постоянных возмущений); улучшение переходных процессов (увеличение быстродействия, максимальное уменьшение динамических ошибок воспроизведения воздействия и от возмущений).