Можно показать, что если выполняется условие (6.20), то среди Pi найдется хотя бы одно, для которого справедливо условие IPi I > 1 Это означает, что система является неустойчивой.

Если соотношение (6.20) не удовлетворяется, никаких выводов относительно принадлежности исследуемой точки к области неустойчивости сделать нельзя. В этом случае можно рассмотреть поведение последовательности следов матрицы В*, т. е.

ISpBI; SpB*;...;SpB*.

Программу рекомендуется строить таким образом, чтобы на каждом шаге возведения матрицы В в степень контролировать условия устойчивости и неустойчивости.

Устойчивость Неустойчивость /В<1; SpB>n:

II ВЧК 1; SpB2>n-,

В*<1; SpB4(>n;

1В2 <1. SpB2 l>n.

m=I,2, 3, ...

Отметим, что функционально-преобразованные матрицы могут иметь различную структуру. Однако bj ьсех случаях алгоритм должен строиться так, чтобы однозначно устанавливалась принадлежность спектра матрицы В кругу радиуса г = 1 с центром в начале координат или некоторой области, вложенной в круг.

Возведение матрицы в степень требует операций умножения и (п - 1) операций сложения. Матричные операции хорошо поддаются распараллеливанию, и современные матричные процессоры позволяют значительно сократить время расчетов. Тем не менее существуют возможности уменьшения трудоемкости за счет изменения вычислительной схемы. Например, в некоторых ЭВМ для перемножения матриц применяется алгоритм Штрассена, в котором число операций умножения составляет /г °& = /г*, а число сложений 6п* - - п. Практически алгоритм Штрассена более эффективен лишь на высоких порядках матрицы.

§ 6.4. Матричный критерий устойчивости, не связанный с обращением матрицы

Вычислительные трудности, связанные с нахождением коэффициентов характеристического полинома по исходной матрице А уравнений переменных состояний пробудили интерес к машинно-ориентированным методам анализа устойчивости, в которых отсутствуют не только операция построения характеристического полинома, но и операция обращения матрицы. Операции обращения, где это возможно, желательно избегать.

В матричном критерии (6.13) в функционально-преобразованную матрицу В входит обратная матрица. Ее появление связано с использованием дробно-линейного преобразования (6.9). Рассмотрим подход в общем случае, устраняющий операцию обращения.

Вообразим себе, что мнимая ось является окружностью бесконечного радиуса. Изогнув ее, получим окружность конечного радиуса. Таким образом приходим к идее охвата области расположения спектра St матрицы А кругом. В дальнейшем такой круг отображается на единичный круг с центром в начале координат комплексной плоскости р или на некоторую область, расположенную внутри этого круга.

Пусть на плоскости s имеется круг радиуса R, в котором содержатся все собственные числа Si матрицы А. Центр круга находится на вещественной отрицательной полуоси в точке 1-R, 0]. Отобразим круг в левой полуплоскости на единичный круг плоскости р с помощью функции

s = /?(p-l). (6.21)

Подставим значение (6.21) в характеристическое уравнение (6.7). После несложных преобразований получим

B-pEl=0, (6 22)

В = Е + А ?. (6.23)

Тогда если все собственные числа S; матрицы А находятся внутри круга радиуса R в левой полуплоскости комплексного переменного 5, то все собственные числа pt функционально-преобразованной матрицы В лежат внутри круга единичного

радиуса с центром в начале координат на плоскости комплексного переменного р, т. е. IpJ < 1 (i = 1, п).

Имеет место следующее утверждение: для того чтобы все собственные числа St (i - 1, 2, п) исходной матрицы коэффициентов А системы (6.7) находились внутри заданного круга радиуса R, расположенного в левой полуплоскбсти и имеющего центр в точке I-R, 01, необходимо и достаточно, чтобы вьтолнялось условие

lim В:

fe->co

(6.24)

где В = Е 4 А ?; О - нулевая матрица.

Таким образом, условие принадлежности всех собственных чисел матрицы А кругу радиуса R, расположенному в левой полуплоскости, сводится к возведению функционально-преобразованной , матрицы В в степень и к изучению последовательности степеней по нормам и модулю следа. Аналогично может быть построен критерий с учетом произвольной степени устойчивости Т].

Пусть задан круг с центром в точке [-R - т], 01, в котором находятся все собственные числа матрицы А (рис. 6.1). Отображая этот круг на единичный круг с центром в начале координат, можно построить функционально-преобразованную матрицу.

Для того чтобы все собственные числа Sj матрицы А системы (6.7) лежали в левой полуплоскости внутри круга радиуса R с центром в точке 1-R -г\, 01, необходимо и достаточно, чтобы удовлетворялось требование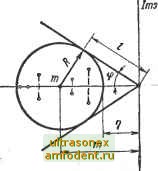

lim В? = О,

к-уоо

Рис. 6.1

Bi = E-b(A-riE) ?; О -нулевая матрица.

Первоначальное значение радиуса может быть выбрано исходя из свойств конкретной исследуемой системы, когда представляется каким-либо образом косвенно оценить частоту ко-