

 |
 |
|
Главная страница Векторные методы процессов jV(w) -]U(w) УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ § 3.1. Понятие устойчивости На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях. В простейшем случае понятие устойчивости системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели, а либо удаляется от него, либо совершает вокруг него недопустимо большие колебания. Наблюдения показывают, что некоторые положения равновесия системы устойчивы к небольшим возмущениям, а другие принципиально возможные равновесные положения практически не могут быть реализованы. Наглядно устойчивость равновесия представлена на рис. 3.1, где изображен шар, расположенный в некотором углублении (рис. 3.1, а), на некоторой выпуклой поверхности (рис. 3.1, б), на плоскости (рис. 3.1, б). Положение равновесия шара характеризуется точкой А о. В случае, изображенном на рис. 3.1, а, при всяком откло- нении шара от положения равновесия, например в точку Ai, он будет стремиться снова возвратиться к положению равновесия - в точку Л о <при отсутствии сил трения) или к некоторой конечной области, окружающей положение равновесия, например в точку А (при наличии сил трения). Такое положение равновесия устойчиво. Случай, изображенный на рис. 3.1, б, соответствует неустойчивому положению равновесия. Рис. 3.1, в соответствует безразличному равновесию. На рис. 3.1, г состояние равновесия устойчиво лишь до тех пор, пока отклонение не вышло за некоторую границу, определяемую, например, точкой В. Выйдя за эту границу, шар уже не вернется в точку Л о, а будет двигаться вправо от точки В либо все время удаляясь, либо до нового состояния равновесия в зависимости от формы поверхности, т. е. в конечном счете в зависимости от уравнений движения шара. Поэтому в общем случае, рассматривая нелинейные системы, вводят понятие устойчивости в малом , в большом в целом . Система устойчива в малом , если констатируют лишь факт наличия области устойчивости, но не определяют каким-либо образом ее границы. Систему называют устойчивой в большом , когда определены границы области устойчивости, т. е. определены границы области начальных отклонений, при которых система возвращается в исходное состояние, и выяснено, что реальные начальные отклонения принадлежат этой области. В том случае, когда система возвращается в исходное состояние при любых начальных отклонениях, систему называют устойчивой б целом . Устойчивость в целом для определенного класса нелинейностей называют абсолютной устойчивостью. Так, например, случай, изображенный на рис. 3.1, а, соответствует устойчивости в целом , а случай, изображенный на рис. 3.1, г, может соответствовать. либо устойчивости в большом , либо устойчивости в малом . Очевидно, что система, устойчи- Рис 31 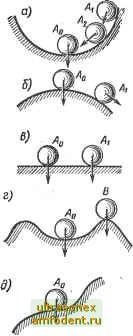 вая в целом , будет устойчива в большом и в малом ; система, устойчивая в большом , будет устойчива и в малом . На рис. ЗА, д изображено еще одно принципиально возможное для нелинейных систем состояние равновесия, которое называют полу устойчивым. Для того чтобы дать определение устойчивости равновесия, вводят понятие о невозмущенном состоянии равновесия, соо--ветствующем состоянию покоя в точке Л о на рис. 3.1, а, и возмущенном состоянии, соответствующем, например, точке Ау, в которую внешняя сила привела шар и затем прекратила свое действие. Система будет устойчивой, если из возмущенного состояния она перейдет в некоторую заданную область, окружающую невозмущенное состояние равновесия. В рассмотренном выше примере с шаром вопрос об устойчивости решается довольно просто. Однако следует заметить, что в общем случае далеко не всегда ясно, при каких условиях равновесное положение системы будет устойчивым. Понятие устойчивости можно распространить и на более общий случай, когда в качестве невозмущенного состояния рассматривают не положение равновесия системы, а ее движение, например движения системы по некоторой наперед заданной траектории. Допустим, что заданное движение системы при отсутствии возмущений должно определяться некоторым законом изменения независимых координат у\ (t), yl (t), уп {t). По аналогии со случаем равновесия положения, заданное движение называют невозмущенным движением. Внешние возмущения, действующие на систему, вызовут отклонение действительного движения системы от заданного. Действительное движение системы называют возмущённым движением. Пусть действительное движение системы определяется независимыми координатами Уу (t), г/2 (О, Уп {() В общем случае уу (t) фу\ (t), y2{t)yl{t), УпЦ)фу1(1). Заданноеевозмущенное движение будет устойчивым, если после приложения внешних мил (возмущений), которые затем снимают, .возмущенное движение по истечении некоторого времени войдет в заданную область \у1 (t) - у! {t)\ Ej, где Ef =-const - заданные величины, i = 1,2,..., п. Чтобы проиллюстрировать сказанное, предположим, что невозмущенное движение происходит по траектории А, а возмущенное движение происходит по траектории Б (рис. 3.2, а). Возьмем на этих траекториях две произвольные точки Л и Л, отвечающие одному и тому же моменту времени /. При
|
|
© 2000 - 2025 ULTRASONEX-AMFODENT.RU.
Копирование материалов разрешено исключительно при условии цититирования. |