идя по мнимой оси при изменении частоты ю от-оо до оо, обходят начало координат в плоскости корней справа по полуокружности бесконечно малого радиуса г (рис. 3.15), т. е. считают не S = О, а S = ге (*-*- О, - я/2 <уя/2).

Тогда все нулевые корни дадут точно такой же угол поворота, как левые корни, т. е. каждый из векторов повернегся на я, и формулы (3.54) и (3.55) сохраняют свою силу.

Обходу начала координат по малой дуге г е в плоскости корней соответствует передаточная функция разомкнутой си-стерлы

F(s) = -

R(0)

Qi (0) (reT

(3.75)

где 6 i и c - свободные члены полиномов R (s) и Qy (s).

При r 0 модуль -> oo, a аргумент \p рленяется от vя/2 до - vя/2 при изменении у от - - я/2 до я/2. Таким образорл, во время движения по полуокружности бесконечно рлалого радиуса в плоскости корней частотная передаточная функция разомкнутой системы W (jo) может быть представлена в виде вектора бесконечно большой длины, поворачивающегося на комплексной плоскости по часовой стрелке на угол, равный-

- vя (от vn/2 до -vn/2).

При изменении ю от О до оо, т. е. при г О и О < Y =я/2, частотная передаточная функция W (/ю) будет изменяться по дуге бесконечно большого радиуса, описывая угол от О до

- vn/2. На рис. 3.16 показана амплитудно-фазовая характе-

Рис. 3.15

Рис. 3.16

lUCo))

Рис. 3.17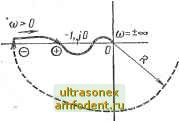

Рис. 3.18

ристика разомкнутой аста- jVCco)

тической системы с аста-тизмом первого порядка

V = 1.

На основе сказанного выше для определения устойчивости систем с аста-тизмом любого порядка v достаточно построить одну ветвь амплитудно-фазовой характеристики разомкнутой системы, соответствующую положительным частотам, дополнить ее дугой - vn/2 окружности бесконечно большого радиуса и затем применить критерий устойчивости Найквиста.

Например, если разомкнутая астатическая система неустойчива, то

замкнутая система будет устойчива, если при изменении частоты (О от О до оо амплитудно-фазовая характеристика разомкнутой астатической системы W (/со), дополненная дугой - vn/2 бесконечно большого радиуса, охватит точку (-1, /0) в положительном направлении 1/2, раз, где / - число правых корней характеристического уравнения разомкнутой системы.

На рис. 3.17 приведена амплитудно-фазовая характеристика разомкнутой системы с астатизмом второго порядка v = 2. Замкнутая система в этом случае будет неустойчива, так как амплитудно-фазовая характеристика W (/со), дополненная дугой - vn/2 = - л бесконечно большого радиуса, всегда охватывает точку (-1, /0) в отрицательном направлении (по часовой стрелке).

На рис. 3.18 приведена амплитудно-фазовая характеристика разомкаутой системы с астатизмом второго порядка, которая после дополнения ее дугой - vn/2 = - л бесконечно большого радиуса не охватывает точку (- 1, /0) (число положительных и отрицательных переходов через отрезок (- оо, -1) равно нулю). Следовательно, замкнутая система будет устойчива. .

Одним из достоинств критерия.Найквиста является то, что он может быть применен и в тех практически важных случаях, когда неизвестны уравнения некоторых звеньев системы либо даже неизвестно уравнение всей разомкнутой системы в целом, но амплитудно-фазовая характеристика разомкнутой системы может быть получена экспериментально. Кроме того, критерий Найквиста позволяет, как это будет показано ниже, довольно просто исследовать устойчивость систем с запаздыванием.

Так как параметры системы определяют обычно приближенно и в процессе работы они могут изменять свое значение, то важна оценка удаления амплитудно-фазовой характеристики разомкнутой системы W (/со) от точки (-1, /0). Это удаление определяет запас устойчивости, который характеризуется двумя величинами: запасом устойчивости по фазе и запасом устойчивости по ам-

со-0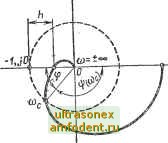

Рис. 3.19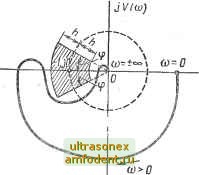

U{W)

плитуде.

Запас устойчивости по фазе определяют как величину угла ф = я - [чр (сос) для частоты сОс, при которой \W (со)с = 1; по амплитуде - как величину отрезка сх;и абсцисс h, заключенного между критической точкой (-1, / 0) и амплитудно-фазовой характеристикой (рис. 3.19).

С ростом коэффициента усиления разомкнутой системы модуль амплитудно-фазовой характеристики также растет и при некотором значении коэффициента усиления К = Ккх называемого критическим коэффициентом усиления, амплитудно-фазовая характеристика пройдет через точку (-1, /0), т. е. система будет на границе устойчивости. При К > Ккр система будет неустойчива.