L(W)

гоьдн

hit)

и lg(w) *

Рис. 2.4

Проходит на уровне L (со) = 20 Ig k. Переходная характеристика (рис. 2.4, в) параллельна оси времени и проходит на уровне h - k.

Интегрирующее звено. Интегрирующим называют звено, которое описывается уравнением ру = ku или передаточной функцией W (s) = kis.

Частотная передаточная функция W (/а) = klj о == = - jklft). Остальные частотные и временные функции имеют следующий вид:

V (со) = 0; V (о)) = - й/со; Д (со) = /со; ф (ю) = = - л/2; L (со) = 20 Ig -20 Igco; h (t) = kt; w (f) = k.

Амплитудно-фазовая частотная характеристика (рис. 2.5, а) интегрирующего звена совпадает с отрицательной мнимой полуосью. ЛФЧХ (рис. 2.5, б) параллельна оси частот и проходит на уровне ф = - л/2; сдвиг фазы не зависит от частоты и равен - я/2. ЛАЧХ (рис. 2.5, б) - наклонная прямая, проходящая через точку с координатами со= 1 и L (со) = 20 Igft. Как видно из уравнения L (со) = 20 \gk- 20 Ig со, при увеличении частоты на одну декаду ордината L (со) уменьшается на 20 дБ. Поэтому наклон ЛАЧХ равен - 20 дБ/дек (читается: минус двадцать децибел на декаду). Переходная характеристика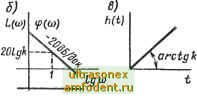

-я/г

представляет собой прямую, проходящую через начало координат с угловым коэффициентом наклона, равным k (рис. 2.5, в).

Дифференцирующее звено. дифференцирующим называют звено, которое описывается уравнением у ~ kpu или Частотные и

201дк

IgO)

Рис. 2.6

передаточной функцией W (s) = ks. временные функции имеют следующий вид:

W (/to) = ]Ы; и (to) == 0; У (to) = Ы; А (to) = кщ Ф (to) = я/2; L (to) = 20 Ig + 20 Ig to; ft (/) = б {t)\ w (/)=

Амплитудно-фазовая частотная характеристика (рис. 2.6,c) совпадает с положительной мнимой полуосью. ЛфЧХ (рис. 2.6,6) параллельна оси частот и проходит на уровне Ф = л/2; сдвиг фазы не зависит от частоты и равен я/2. ЛАЧХ есть прямая, проходшдая через точку с координатами ю = 1 и L(to) - 20 Ig ft и имеющая наклон 20 дБ/дек (читается: плюс двадцать децибел на декаду); L (ш) увеличивается на 20 дБ при увеличении частоты на одну декаду.

Апериодическое звено. Апериодическим звеном первого порядка называют звено, которое описывается уравнением

{Тр + 1) у = ku (2.44)

или передаточной функцией

W (S) = kl{Ts +1).

Это звено также называют инерционным звеном или инерционным звеном первого порядка. Апериодическое звено в отличие от вышерассмотренных звеньев характеризуется двумя параметрами: постоянной времени Т и передаточным коэффициентом k.

Частотная передаточная функция

W (/to) = fe/(r/to + 1). (2.45)

Умножив числитель и знаменатель на комплексно-сопряженное знаменателю число, получим

и (to) = ft/[(Tto) + 11; V (to) = - feTto/KTto) -f П. (2.46)

Амплитудную и фазовую частотные функции можно определить, воспользовавшись правилом модулей и аргументов.

Так как модуль числителя частотной передаточной функции (2.45) равен к, а модуль знаменателя 1/(7 со) + 1, то

A(a)=k/V{Taf+l.

(2.47)

Аргумент числителя W (/со) равен нулю, а аргумент знаменателя arctg ю7, поэтому ф (to) = arg W (/со) = - arctg (лТ. Из (2.47).

L (со) = 20 Ig Л (со) = 20 Ig ft-20 IgViTaf + 1 - (2.48)

Решив дифференциальное уравнение (2.44) при м = 1 (О и нулевом начальном условии (х (0) = 0), получим ft (t) - = ft (1 - е -/). Весовая функция

и, (О = А (О-(ft/Tie-/-.

АФЧХ апериодического звена (рис. 2.7, а) есть полуокружность, в чем нетрудно убедиться, исключив из параметрических уравнений (2.46) АФЧХ частоту.

Логарнфлическая амплитудно-частотная характеристика представлена на рис. 2.7, б. На практике обычно ограничиваются построением так называемой асимптотической ЛАЧХ (ломаная линия на том же рис. 2.7, б). Только в критических случаях, когда небольшая погрешность может повлиять на выводы, рассматривают точную ЛАЧХ. Впрочем, точную ЛАЧХ можно легко построить по асимптотической ЛАЧХ если вос-

WlgK

К и

<w-0

11,Е 1 2 t

Ё IB 1SW ш W sm W во

да Dj)2 от 0,1 в,г т ол i

85 В7в8 S3 В5А ifMepad

еда го чо вв wo rw