то и переходный процесс h (t) может быть представлен суммой составляющих:

h{t)h,it). (4.76)

2. Соответствие масштабов по оси ординат для Р (со) и h (О- Если умножить Р (со) на постоянный множитель а, то соответствующие значения h (t) тоже умножаются на этот множитель а.

3. Соответствие масштабов по оси абсцисс для Р (со) и h (t). Если аргумент со в соответствующем выражении частотной характеристики умножить на постоянное число (рис. 4.23, а), то аргумент и в соответствующем выражении переходного процесса будет делиться на это число (рис. 4.23, б), т. е.

h (t/a) = - f -- sin cocfco. (4.77)

4. Начальное значение вещественной частотной характеристики равно конечному значению переходной характеристики:

lim Р (со) = lim х (t) = lim h (t).

03->0 t-co t~>oo

Начальное значение мнимой частотной характеристики <3 (0) = 0.

5. Конечное значение вещественной частотной характеристики равно начальному значению оригинала переходной ха-

рактеристики:

t- lira Р И = Ип! X {t) lim h (t).

Представляют интерес разрывы непрерывности и пики в вещественной частотной характеристике. Пред-

Луг/77=1-/-/NsX:- положим, что прИ СО = COj

вещественная частотная характеристика имеет разрыв непрерывности Р (со) = с , при этом характеристическое уравнение системы будет Рис. 4.23 иметь мнимый корень s,- =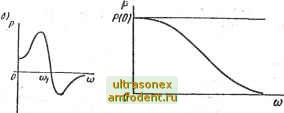

Рис. 4.24

Рис. 4.25

= ±/b)i, Т. е. В системе устанавливаются незатухающие гармонические колебания, если остальные корни левые. Характеристика для этого случая показана на рис. 4.24, а. По-видимому, высокий и острый пик частотной характеристики, за которым Р (со) переходит через нуль, при частоте, близкой к о>1, соответствует медленно затухающим колебаниям (рис. 4.24, б).

6. Чтобы переходная характеристика системы имела перерегулирование, не превышающее 18 % (а < 18 9-), веш,ест-венная частотная характеристика должна быть положительной невозрастающей функцией частоты (рис. 4.25), т. е. Р (со) > О, dP ((o)/doi < 0.

7. Условия монотонного протекания переходного процесса. Чтобы переходный процесс имел монотонный характер, достаточно, чтобы соответствующая

ему вещественная частотная характеристика Р (со) была положительной, непрерывной функцией частоты с отрицательной, убывающей по абсолютному значению производной (рис. 4.26, а, б), т. е.

Р (со) > О, [dP (co)/rfco] < 0.

8. Определение наибольшего значения перерегулирования а ах переходного процесса по максимуму вещественной частотной характеристики Р (со) (рис. 4:27):

а,г.ах == Ц Д8Р ,х-Р (0)J/P (0), (4.78)

где Рпак - максимальное значение Р (со); Р (0) - начальное значение

(со = 0). Рис. 4.26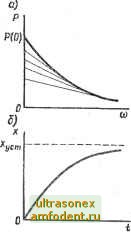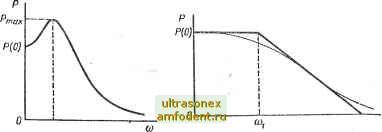

щ со

Рис. 4 27

Рис. 4.28

9. Если вещественная частотная характеристика близка к трапецеидальной, т. е. может быть аппроксимирована трапецией с диапазоном частот cog и коэффициентом наклона % = = coi/coa (рис. 4.28), то время регулирования переходного процесса системы заключено в пределах я/соа < < 4jt/co2.

Оценить время регулирования tp и перерегулирование можно по кривым, приведенным на рис. 4.29. Это применимо для систем с невозрастающей вещественной частотной характеристикой.

Если вещественная частотная характеристика Р (со) имеет максимум Ртах. ТО перерегулированис а в и время регулирования оценивают по кривым рис. 4.30, а, б в зависимости от отношения PmaJP Ф)- При ЭТОМ время регулирования заключено в пределах Ззх/сог, < tp < 8л;/сог.

Остановимся на приближенном методе построения графиков переходных процессов в системе по вещественным частотным характеристикам при воздействии единичной функции

g (t) = I (t) и нулевых на-

20 16

чальных условиях.

Метод трапеций. В инженерной практике широко применяют метод разложения частотной характеристики на сумму трапеций, предложенный В. В. Солодовниковым. Две сюроны единичной трапеции Б (рис. 4.31) совпадают 0,2 OA 0,6 0,6 W X. с координатными осями, фетья параллельна оси аб-Рис. 4.29 сцисс, а четвертая имеет